题目内容
1.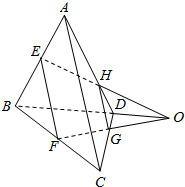 如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.
如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.
分析 由已知得EF与GH平行且不相等,从而E、F、G、H四点共面,且EH∩FG=O,由此利用公理二能证明直线EH,FG和BD共点.
解答 证明:∵在空间四边形ABCD中,E、F分别是AB、BC的中点,
G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,
∴GH∥AC,且GH=$\frac{1}{3}$AC,
EF∥AC,且EF=$\frac{1}{2}AC$,
∴EF与GH平行且不相等,
∴E、F、G、H四点共面,∴EH∩FG=O,如图,
∵E,H∈平面ABD,F,G∈平面BDC,平面ABD∩平面BDC=BD,
∴O∈BD,∴直线EH,FG和BD共点.
点评 本题考查三线共点的证明,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
12.已知等差数列{an}满足a3=7,a5+a7=26,则通项公式an=( )
| A. | 2n-1 | B. | 2n+1 | C. | 3n+1 | D. | 4n+1 |
10.定义在(0,+∞)上的单调递减函数f(x),若f(x)的导函数存在且满足$\frac{f(x)}{f'(x)}>-x$,则下列不等式成立的是( )
| A. | 3f(2)<2f(3) | B. | 3f(3)>4f(4) | C. | 3f(4)<4f(3) | D. | f(2)<2f(1) |
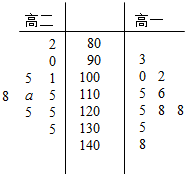 高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)
高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)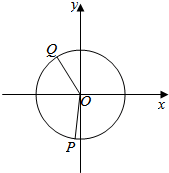 角α和β的顶点为平面直角坐标系的原点,始边都与x轴的正半轴重合,终边分别与单位圆(半径为1)相交于点P、Q两点,已知Q点也在射线y=-$\frac{4}{3}$x(x<0)上.
角α和β的顶点为平面直角坐标系的原点,始边都与x轴的正半轴重合,终边分别与单位圆(半径为1)相交于点P、Q两点,已知Q点也在射线y=-$\frac{4}{3}$x(x<0)上.