题目内容
10.定义在(0,+∞)上的单调递减函数f(x),若f(x)的导函数存在且满足$\frac{f(x)}{f'(x)}>-x$,则下列不等式成立的是( )| A. | 3f(2)<2f(3) | B. | 3f(3)>4f(4) | C. | 3f(4)<4f(3) | D. | f(2)<2f(1) |
分析 由题意构造g(x)=xf(x),求出g′(x),化简已知的式子后,结合题意判断出g′(x)的符号,可得g(x)在(0,+∞)上的单调性,由函数的单调性可得答案.
解答 解:设g(x)=xf(x),则g′(x)=f(x)+xf′(x),
因为定义在(0,+∞)上的单调递减函数f(x),
所以x∈(0,+∞)时,f′(x)<0,
由$\frac{f(x)}{f′(x)}>-x$得$\frac{f(x)}{f′(x)}+x>0$,则$\frac{xf′(x)+f(x)}{f′(x)}>0$,
则当∈(0,+∞)时,f(x)+xf′(x)<0,即g′(x)<0,
所以函数g(x)在(0,+∞)上递减,
则g(3)>g(4),即3f(3)>4f(4),
故选:B.
点评 本题考查函数的单调性与导数的关系,以及构造函数法,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
20.p:x2=3x-2是q:x=$\sqrt{3x-2}$的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
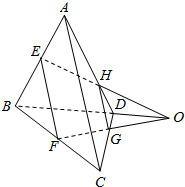 如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.
如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.