题目内容
9.若函数y=f(x)定义域是R.则①函数y=f(x)与函数y=-f(x)的图象关于x轴对称;
②函数y=f(x-1)与函数y=f(1-x)的图象关于直线x=1对称:
③函数y=f(x-1)与y=-f(1-x)的图象关于($\frac{1}{2}$,0)对称.
④函数y=f(2x+1)的图象与y=f(3-2x)的图象关于直线x=2对称.
分析 根据函数y=f(a+x)与函数y=f(b-x)的图象关于直线x=$\frac{a+b}{2}$对称,定义在R上的函数f(x)关于点(a,b)对称的充要条件是f(x)+f(2a-x)=2b
解答 解:①∵函数y=f(x)与函数y=-f(x)的图象关于x轴对称;
②∵函数y=f(x-1)的图象关于直线x=a对称的图象解析式为
y=f[(2a-x)-1)]=f(2a-1-x)
令2a-1=1
得a=1
即函数y=f(x-1)和y=f(1-x)的图象关于直线x=1对称;
③:定义在R上的函数f(x)关于点(a,b)对称的充要条件是f(x)+f(2a-x)=2b
∵f(x-1)=-f(1-x),
∴f(x)+f(1-x)=0,
∴2a=1,2b=0即a=$\frac{1}{2}$,b=0,
∴函数f(x)关于点($\frac{1}{2}$,0)对称:
④f(2x+1)=f(3-2x),
∴x=$\frac{1}{2}$(1+3)=2,
∴函数y=f(2x+1)的图象与y=f(3-2x)的图象关于直线x=2对称.
故答案为:①x轴,②直线x=1,③($\frac{1}{2}$,0),④直线x=2.
点评 本题主要考查了抽象函数及其应用,以及函数图象的对称等有关知识,属于基础题.

练习册系列答案
相关题目
14.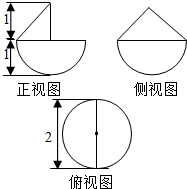 某几何体的三视图如图所示.则该几何体的体积为( )
某几何体的三视图如图所示.则该几何体的体积为( )
 某几何体的三视图如图所示.则该几何体的体积为( )
某几何体的三视图如图所示.则该几何体的体积为( )| A. | π | B. | $\frac{3π}{2}$ | C. | $\frac{5π}{3}$ | D. | $\frac{5π}{6}$ |
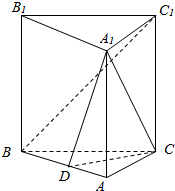 在正三棱柱ABC-A1B1C1中,点D是AB的中点,证明:
在正三棱柱ABC-A1B1C1中,点D是AB的中点,证明: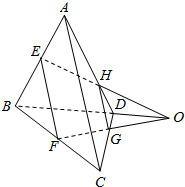 如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.
如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.