题目内容
11.设点P是双曲线${x^2}-\frac{y^2}{3}=1$上一点,焦点F(2,0),点A(3,2),使4|PA|+2|PF|有最小值时,则点P的坐标是$(\frac{{\sqrt{21}}}{3},2)$.分析 根据题意算出双曲线的离心率e=2,右准线方程为x=$\frac{1}{2}$.连结PF,过P作右准线的垂线,垂足为M,由双曲线第二定义得|PM|=$\frac{1}{2}$|PF|,从而得出|PA|+$\frac{1}{2}$|PF|=|PA|+|PM|,利用平面几何知识可得当P、A、M三点共线时,|PA|+|PM|=|AM|达到最小值.由此利用双曲线的方程加以计算,可得满足条件的点P的坐标.
解答 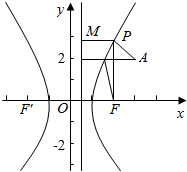 解:∵双曲线${x^2}-\frac{y^2}{3}=1$中,a=1,b=$\sqrt{3}$,
解:∵双曲线${x^2}-\frac{y^2}{3}=1$中,a=1,b=$\sqrt{3}$,
∴c=2,
可得双曲线的离心率e=2,右准线方程为x=$\frac{1}{2}$,
设右准线为l,过P作PM⊥l于M点,连结PF,
由双曲线的第二定义,可得|PM|=$\frac{1}{2}$|PF|.
∴|PA|+$\frac{1}{2}$|PF|=|PA|+|PM|,
运动点P,可得当P、A、M三点共线时,|PA|+|PM|=|AM|达到最小值.
此时经过P、A、M三点的直线与x轴平行,
设P(m,2),代入双曲线方程得m=$\frac{\sqrt{21}}{3}$,得点P($\frac{\sqrt{21}}{3}$,2).
∴满足使4|PA|+2|PF|=4(|PA|+$\frac{1}{2}$|PF|)有最小值的点P坐标为$(\frac{{\sqrt{21}}}{3},2)$.
故答案为:$(\frac{{\sqrt{21}}}{3},2)$.
点评 本题给出定点A与双曲线上的动点P,求4|PA|+2|PF|有最小值时点P的坐标.着重考查了双曲线的定义与标准方程、简单几何性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知全集U={1,2,3,4,5,6},集合A={1,3,5,6},则∁UA等于( )
| A. | {1,3,5} | B. | {2,4,6} | C. | {2,4} | D. | {1,3,5,6} |
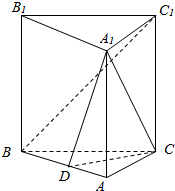 在正三棱柱ABC-A1B1C1中,点D是AB的中点,证明:
在正三棱柱ABC-A1B1C1中,点D是AB的中点,证明: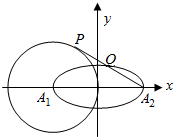 如图平面直角坐标系xOy中,椭圆$\frac{x^2}{4}+{y^2}=1$,A1,A2分别是椭圆的左、右两个顶点,圆A1的半径为2,过点A2作圆A1的切线,切点为P,在x轴的上方交椭圆于点Q.则$\frac{PQ}{Q{A}_{2}}$=$\frac{3}{4}$.
如图平面直角坐标系xOy中,椭圆$\frac{x^2}{4}+{y^2}=1$,A1,A2分别是椭圆的左、右两个顶点,圆A1的半径为2,过点A2作圆A1的切线,切点为P,在x轴的上方交椭圆于点Q.则$\frac{PQ}{Q{A}_{2}}$=$\frac{3}{4}$.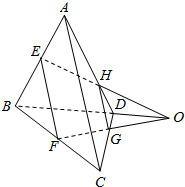 如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.
如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.