题目内容
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最，编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”，见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注，还得到了无数外国人的关注.某单位有10位外国人，其中关注此次大阅兵的有8位，若从这10位外国人中任意选取3位做一次采访，则被采访者中至少有2位关注此次大阅兵的概率为（ ）
A.
B.
C.
D.
【答案】C
【解析】
至少有2位关注此次大阅兵的对立事件为恰有2位不关注此次大阅兵，根据对立事件的概率公式计算概率.
解：从这10位外国人中任意选取3位做一次采访，其结果为
个，
恰有2位不关注此次大阅兵有
个，
则至少有2位关注大阅兵的概率
.
故选：
【题目】某校高三实验班的60名学生期中考试的语文、数学成绩都在
内，其中语文成绩分组区间是：
，
，
，
，
.其成绩的频率分布直方图如图所示，这60名学生语文成绩某些分数段的人数
与数学成绩相应分数段的人数
之比如下表所示：
分组区间 |
|
|
|
|
|
|
|
|
|
| |
24 | 3 | ||||
数学人数 | 12 | 4 |
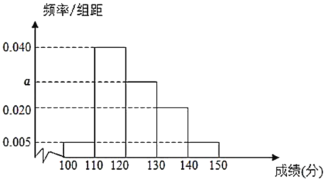
（1）求图中
的值及数学成绩在的人数；
（2）语文成绩在的3名学生均是女生，数学成绩在的4名学生均是男生，现从这7名学生中随机选取4名学生，事件
为：“其中男生人数不少于女生人数”，求事件发生的概率；
（3）若从数学成绩在
的学生中随机选取2名学生，且这2名学生中数学成绩在的人数为
，求的分布列和数学期望
.
【题目】某公司准备投产一种新产品，经测算，已知每年生产
万件的该种产品所需要的总成本
（万元），依据产品尺寸，产品的品质可能出现优、中、差三种情况，随机抽取了1000件产品测量尺寸，尺寸分别在
，
，
，
，
，
，
（单位：
）中，经统计得到的频率分布直方图如图所示.
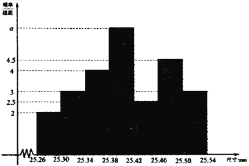
产品的品质情况和相应的价格
（元/件）与年产量
之间的函数关系如下表所示.
产品品质 | 立品尺寸的范围 | 价格 |
优 |
|
|
中 |
|
|
差 |
|
|
以频率作为概率解决如下问题：
（1）求实数
的值；
（2）当产量确定时，设不同品质的产品价格为随机变量
，求随机变量的分布列；
（3）估计当年产量为何值时，该公司年利润最大，并求出最大值.
