题目内容
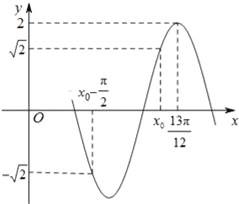
【题目】已知曲线C的极坐标方程是ρ=6sinθ,建立以极点为坐标原点,极轴为x轴正半轴的平面直角坐标系.直线l的参数方程是![]() ,(t为参数).
,(t为参数).
(1)求曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点,且|AB|=![]() ,求直线的斜率k.
,求直线的斜率k.
【答案】(1) ![]() . (2)
. (2) ![]() .
.
【解析】
(1)运用x=ρcosθ,y=ρsinθ,即可将曲线C的极坐标方程化为直角坐标方程;
(2)方法1:化直线的参数方程为普通方程,再由条件,即可得到直线方程,再求出圆心到直线的距离,结合|AB|=![]() ,利用勾股定理,即可求出直线的斜率;方法2:直接把直线的参数方程代入圆,运用韦达定理,计算
,利用勾股定理,即可求出直线的斜率;方法2:直接把直线的参数方程代入圆,运用韦达定理,计算![]() ,结合|AB|=
,结合|AB|=![]() ,即可得到斜率.
,即可得到斜率.
解:(1)由曲线![]() 的极坐标方程是
的极坐标方程是![]() ,得直角坐标方程为
,得直角坐标方程为![]() ,
,
即![]() .
.
(2)把直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),
为参数),
代入圆![]() 的方程得
的方程得![]() ,
,
化简得![]() .
.
设![]() 两点对应的参数分别是
两点对应的参数分别是![]() ,则
,则![]() ,
,![]()
故![]()
得![]() ,
,
得![]() .
.

【题目】近年来,我国工业经济发展迅速,工业增加值连年攀升,某研究机构统计了近十年(从2008年到2017年)的工业增加值(万亿元),如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工业增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依据表格数据,得到下面的散点图及一些统计量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
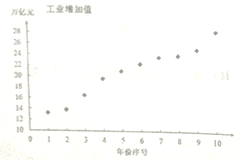
(1)根据散点图和表中数据,此研究机构对工业增加值![]() (万亿元)与年份序号
(万亿元)与年份序号![]() 的回归方程类型进行了拟合实验,研究人员甲采用函数
的回归方程类型进行了拟合实验,研究人员甲采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员乙采用函数
;研究人员乙采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员丙采用线性函数
;研究人员丙采用线性函数![]() ,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数
,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数![]() 与拟合指数
与拟合指数![]() 满足关系
满足关系![]() ).
).
(2)根据(1)的判断结果及统计值,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)预测到哪一年的工业增加值能突破30万亿元大关.
附:样本
![]() 的相关系数
的相关系数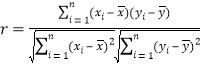 ,
,
![]() ,
,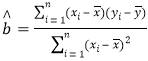 ,
,![]() .
.
【题目】在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶某村![]() 户贫困户.为了做到精准帮扶,工作组对这
户贫困户.为了做到精准帮扶,工作组对这![]() 户村民的年收入情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标
户村民的年收入情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() .将指标
.将指标![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五组,得到如图所示的频率分布直方图.规定若
分成五组,得到如图所示的频率分布直方图.规定若![]() ,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当
,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当![]() 时,认定该户为“亟待帮住户”.工作组又对这
时,认定该户为“亟待帮住户”.工作组又对这![]() 户家庭的受教育水平进行评测,家庭受教育水平记为“良好”与“不好”两种.
户家庭的受教育水平进行评测,家庭受教育水平记为“良好”与“不好”两种.

(1)完成下面的列联表,并判断是否有![]() 的把握认为绝对贫困户数与受教育水平不好有关:
的把握认为绝对贫困户数与受教育水平不好有关:
受教育水平良好 | 受教育水平不好 | 总计 | |
绝对贫困户 |
| ||
相对贫困户 |
| ||
总计 |
|
(2)上级部门为了调查这个村的特困户分布情况,在贫困指标处于![]() 的贫困户中,随机选取两户,用
的贫困户中,随机选取两户,用![]() 表示所选两户中“亟待帮助户”的户数,求
表示所选两户中“亟待帮助户”的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|