��Ŀ����
����Ŀ��ijУ����ʵ����60��ѧ�����п��Ե����ġ���ѧ�ɼ�����![]() �ڣ��������ijɼ����������ǣ�
�ڣ��������ijɼ����������ǣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
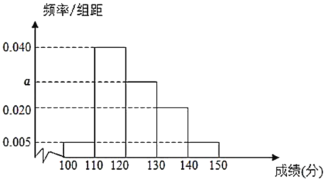
��![]() .��ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����60��ѧ�����ijɼ�ijЩ�����ε�����
.��ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����60��ѧ�����ijɼ�ijЩ�����ε�����![]() ����ѧ�ɼ���Ӧ�����ε�����
����ѧ�ɼ���Ӧ�����ε�����![]() ֮�����±���ʾ��
֮�����±���ʾ��
�������� |
|
|
|
|
|
|
|
|
|
| |
24 | 3 | ||||
��ѧ���� | 12 | 4 |
��1����ͼ��![]() ��ֵ����ѧ�ɼ���
��ֵ����ѧ�ɼ���![]() ��������
��������
��2�����ijɼ���![]() ��3��ѧ������Ů������ѧ�ɼ���
��3��ѧ������Ů������ѧ�ɼ���![]() ��4��ѧ�������������ִ���7��ѧ�������ѡȡ4��ѧ�����¼�
��4��ѧ�������������ִ���7��ѧ�������ѡȡ4��ѧ�����¼�![]() Ϊ����������������������Ů�������������¼�
Ϊ����������������������Ů�������������¼�![]() �����ĸ��ʣ�
�����ĸ��ʣ�
��3��������ѧ�ɼ���![]() ��ѧ�������ѡȡ2��ѧ��������2��ѧ������ѧ�ɼ���
��ѧ�������ѡȡ2��ѧ��������2��ѧ������ѧ�ɼ���![]() ������Ϊ
������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() .
.
���𰸡���1����ѧ�ɼ���![]() ������Ϊ8�ˣ�2��
������Ϊ8�ˣ�2��![]() ��3���������
��3���������
��������
��1���ɸ���Ƶ�ʷֲ�ֱ��ͼ�����ʣ����![]() ���ٸ���Ƶ�ʷֲ�ֱ��ͼ���ݣ�������⣻
���ٸ���Ƶ�ʷֲ�ֱ��ͼ���ݣ�������⣻
��2�����¼�![]() �ɷ�Ϊ��2��������2��Ů������3������1��Ů������4������������������������Ӧ�ĸ��ʣ�
�ɷ�Ϊ��2��������2��Ů������3������1��Ů������4������������������������Ӧ�ĸ��ʣ�
��3�������⣬�õ�![]() ����ȡֵ��
����ȡֵ��![]() �������Ӧ�ĸ��ʣ������������ķֲ��У����������Ĺ�ʽ���������.
�������Ӧ�ĸ��ʣ������������ķֲ��У����������Ĺ�ʽ���������.
��1�������⣬����Ƶ�ʷֲ�ֱ��ͼ�����ʣ�
�ɵ�![]() �����
�����![]() .
.
�����ijɼ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �е������ֱ�Ϊ
�е������ֱ�Ϊ![]() ��
��
����ѧ�ɼ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �е������ֱ�
�е������ֱ�
Ϊ![]() ��
��
������ѧ�ɼ���![]() ������Ϊ8��.
������Ϊ8��.
��2������7��ѧ�������ѡȡ4��ѧ�����¼�![]() Ϊ����������������������Ů����������
Ϊ����������������������Ů����������
�ɷ�Ϊ��2��������2��Ů������3������1��Ů������4�����������������
�����¼�![]() �����ĸ���
�����ĸ���![]() .
.
��3���������֪![]() ����ȡֵ��0��1��2.
����ȡֵ��0��1��2.
![]() ��
��![]() ��
��![]() ��
��
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 |
|
|
|
|
����![]() .
.

 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�����Ŀ��һ������ѧ�����������о��ŶӴ�ij��ѧ�����ѡ100��ѧ�����м�����ԣ�ͨ������100��İ�����ʺ����ʮ���ӽ�����д���ԣ����ʱ��![]() �����ӣ��ʹ������
�����ӣ��ʹ������![]() ��ͳ�Ʊ������£�
��ͳ�Ʊ������£�
ʱ�� | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
������� | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
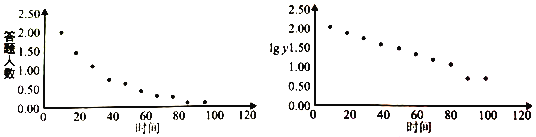
ʱ��![]() ��������
��������![]() ��ɢ��ͼ��ͼ��
��ɢ��ͼ��ͼ��
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������һ������
������һ������![]() ��
��![]() ��������
��������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��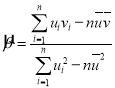 ��
��![]() .����ݱ������ݻش��������⣺
.����ݱ������ݻش��������⣺
��1������ɢ��ͼ�жϣ�![]() ��
��![]() ���ĸ���������Ϊ���Իع����ͣ��������жϼ��ɣ�����˵�����ɣ�
���ĸ���������Ϊ���Իع����ͣ��������жϼ��ɣ�����˵�����ɣ�
��2�����ݣ�1�����жϽ��������![]() ��
��![]() �Ļع鷽�̣������ݱ���3λ��Ч���֣�
�Ļع鷽�̣������ݱ���3λ��Ч���֣�
��3�����ݣ�2�������Ҫ���ס![]() �����ݣ����������ٷ������¼���һ��.���ο����ݣ�
�����ݣ����������ٷ������¼���һ��.���ο����ݣ�![]() ��
��![]() ��
��
����Ŀ��2019��˫ʮһ�����Ļ����è�������268����λ��ʮ��Ԫ������ң���ͬ�����ٴ��¸ߣ���ȥ��218��ʮ��Ԫ������50��ʮ��Ԫ������Щ���ֵı�������������������ı��֣����ǹ��ﳵ���й������ѵ��漣��Ϊ���о��������۶�ı仯���ƣ�һ����ͳ����2010�굽2019����è˫ʮһ�����۶�����![]() ����λ��ʮ��Ԫ��.�������±�1��
����λ��ʮ��Ԫ��.�������±�1��
��1
��� | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
���۶� | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
�����������ݻ���ɢ��ͼ����ͼ��ʾ.
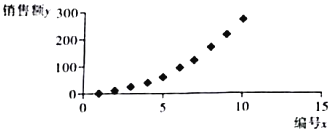
�����۳���100��ʮ��Ԫ������ݽ������������������۶��200��ʮ��Ԫ������ݽ�������������2010�굽2019����ʮ�����������������ȡ2����������ȡ��һ�����������ĸ���.
�ο���ʽ������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ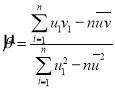 ��
��![]() .
.
