题目内容
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
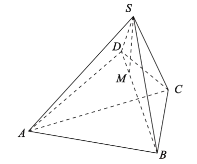
(1)求证:![]() ;
;
(2)若![]() 为线段
为线段![]() 上的一点,
上的一点,![]() ,
,![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)设![]() 交
交![]() 于点
于点![]() ,证明
,证明![]() 平面
平面![]() 内的两条相交直线即可得到线面垂直,再由线面垂直的性质,可证明线线垂直;
内的两条相交直线即可得到线面垂直,再由线面垂直的性质,可证明线线垂直;
(2)找到三条两两互相垂直的直线,以![]() 为原点,以射线
为原点,以射线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正半轴建立空间直角坐标系,求出平面
轴正半轴建立空间直角坐标系,求出平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,求法向量夹角的余弦值,即可求得答案.
,求法向量夹角的余弦值,即可求得答案.
设![]() 交
交![]() 于点
于点![]() ,
,![]()
![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,在
,在![]() 中,
中,
![]() 且
且![]() ,得
,得![]() ,即
,即![]() ,
,
又平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]()
![]()
(2)平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
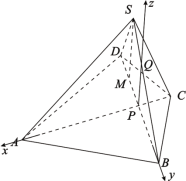
以![]() 为原点,以射线
为原点,以射线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正半轴建立空间直角坐标系,
轴正半轴建立空间直角坐标系,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则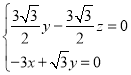 ,
,
取![]() ,得
,得![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则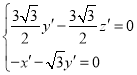 ,取
,取![]() ,得
,得![]() ,
,
设所求角为![]() ,则
,则![]() ,
,
![]() 所求的锐二面角余弦值为
所求的锐二面角余弦值为![]()

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
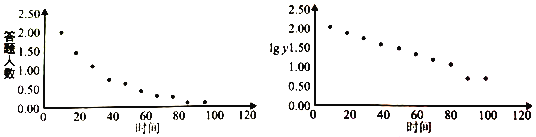
【题目】一个调查学生记忆力的研究团队从某中学随机挑选100名学生进行记忆测试,通过讲解100个陌生单词后,相隔十分钟进行听写测试,间隔时间![]() (分钟)和答对人数
(分钟)和答对人数![]() 的统计表格如下:
的统计表格如下:
时间 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答对人数 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
时间![]() 与答对人数
与答对人数![]() 的散点图如图:
的散点图如图:
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对于一组数据
,对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: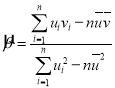 ,
,![]() .请根据表格数据回答下列问题:
.请根据表格数据回答下列问题:
(1)根据散点图判断,![]() 与
与![]() ,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果,建立![]() 与
与![]() 的回归方程;(数据保留3位有效数字)
的回归方程;(数据保留3位有效数字)
(3)根据(2)请估算要想记住![]() 的内容,至多间隔多少分钟重新记忆一遍.(参考数据:
的内容,至多间隔多少分钟重新记忆一遍.(参考数据:![]() ,
,![]() )
)