题目内容
三个不同的数成等差数列,其和为6,如果将此三个数重新排列,他们又可以成等比数列,求这个等差数列。
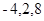 ,或
,或
解析试题分析:可以先将成等差的这三个数设出来,设为 ,由和为
,由和为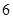 ,可求得
,可求得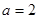 ,重新排列后,又成 等比数列,根据等比中项分类讨论,可解.
,重新排列后,又成 等比数列,根据等比中项分类讨论,可解.
试题解析:设成等差数列的这三个数为 (
(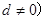 ,则
,则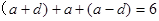 ,∴
,∴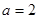 ,这三个数为
,这三个数为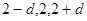 ,
,
当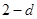 为等比中项时:
为等比中项时: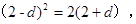 ∴
∴ (舍去),或
(舍去),或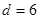 ,等差数列为:-4,2,8.
,等差数列为:-4,2,8.
当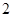 为等比中项时:
为等比中项时: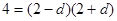 ,∴
,∴ (舍去).
(舍去).
当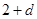 为等比中项时:
为等比中项时: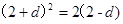 ,∴
,∴ (舍去),或
(舍去),或 ,等差数列为8,2,-4.
,等差数列为8,2,-4.
综上所述:等差数列为-4,2,8,或8,2,-4.
考点:1、等差数列和等比数列运算;2、分类讨论思想.

练习册系列答案
相关题目
 ,
, ,设
,设 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,且首项
,且首项 是
是 中的最大数,
中的最大数,  .
. 满足
满足 ,求
,求 的值.
的值. }中,a1=1,
}中,a1=1, 是数列{
是数列{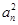 +p
+p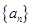 各项为非负实数,前n项和为
各项为非负实数,前n项和为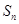 ,且
,且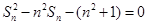
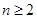 时,求
时,求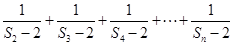 .
. 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 .
. 及
及 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.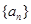 的前
的前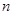 项和为
项和为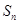 ,且
,且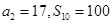 .
.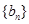 满足
满足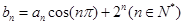 ,求数列
,求数列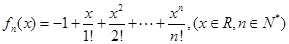
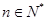 ,存在唯一的
,存在唯一的 ,满足
,满足 ;
;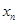 构成数列
构成数列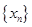 ,判断数列
,判断数列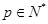 ,
,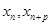 满足(Ⅰ),试比较
满足(Ⅰ),试比较 与
与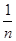 的大小.
的大小.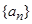 的前
的前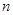 项和为
项和为 ,对任意
,对任意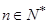 满足
满足 ,且
,且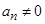 .
. ,求数列
,求数列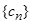 的前
的前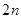 项和
项和 .
. }的前n项和为
}的前n项和为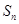 ,
,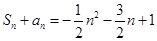 ,
,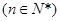 .
. ,证明:数列
,证明:数列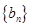 是等比数列;
是等比数列;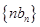 的前
的前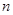 项和
项和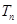 ;
;