题目内容
各项均为正数的数列{ }中,a1=1,
}中,a1=1, 是数列{
是数列{ }的前n项和,对任意n∈N﹡,有2
}的前n项和,对任意n∈N﹡,有2 =2p
=2p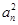 +p
+p -p(p∈R).
-p(p∈R).
(1)求常数p的值;
(2)求数列{ }的前n项和
}的前n项和 .
.
(1)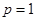 ;(2)
;(2)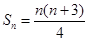 .
.
解析试题分析:(1)因为 ,代入已知条件即可解得
,代入已知条件即可解得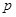 ;(2)由(1)将关系式化简,考虑到是
;(2)由(1)将关系式化简,考虑到是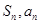 的关系,故可利用
的关系,故可利用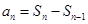 解答,最后利用等差数列前
解答,最后利用等差数列前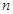 项和公式计算.
项和公式计算.
试题解析:(1)由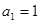 及
及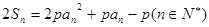 ,
,
得: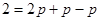 ,
,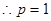 . 4分
. 4分
(2)由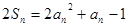 ①
①
得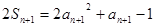 ②
②
由②—①,得 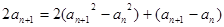 5分
5分
即: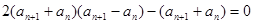 ,
,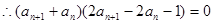 7分
7分
由于数列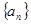 各项均为正数,
各项均为正数, ,即
,即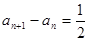 ,
, 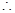 数列
数列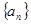 是首项为
是首项为 ,公差为
,公差为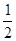 的等差数列, 8分
的等差数列, 8分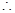 数列
数列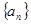 的通项公式是
的通项公式是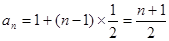 , 10分
, 10分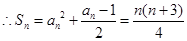 . 12分
. 12分
考点:等差数列通项公式、等差数列前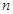 项和公式、
项和公式、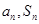 间的关系.
间的关系.

练习册系列答案
相关题目
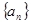 中,若
中,若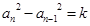 (
(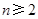 ,
,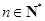 ,
,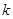 为常数),则称
为常数),则称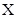 数列.
数列.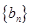 是
是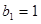 ,
,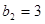 ,写出所有满足条件的数列
,写出所有满足条件的数列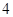 项;
项; 或
或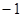 ;
;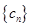 满足
满足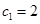 ,
,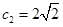 ,
,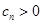 ,设数列
,设数列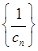 的前
的前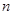 项和为
项和为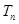 .是否存在
.是否存在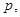
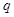 ,使不等式
,使不等式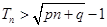 对一切
对一切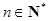 都成立?若存在,求出
都成立?若存在,求出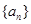 的前3项和
的前3项和 =9,且
=9,且 成等比数列
成等比数列 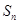 ;
; 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值
的最小值 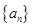 是正数组成的数列,
是正数组成的数列,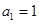 ,且点
,且点 在函数
在函数 的图象上.
的图象上. 满足
满足 ,
, ,求证:
,求证:
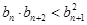 .
.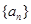 的前
的前 项和为
项和为 ,若
,若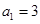 ,点
,点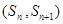 在直线
在直线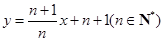 上.
上.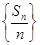 是等差数列;
是等差数列;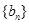 满足
满足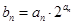 ,求数列
,求数列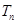 ;
;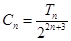 ,求证:
,求证: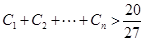 .
. 是首项为
是首项为 ,公差为
,公差为 的等差数列
的等差数列 ,
, 是其前
是其前 项和.
项和. ,
, ,求数列
,求数列 ,
,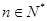 ,且
,且 、
、 、
、 成等比数列,证明:
成等比数列,证明: .
.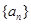 的前
的前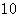 项和
项和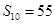 ,且
,且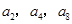 成等比数列.
成等比数列.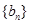 满足
满足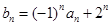 ,求
,求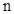 项和
项和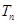 .
.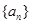 满足:
满足: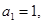 点
点 均在直线
均在直线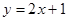 上.
上.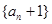 为等比数列,并求出数列
为等比数列,并求出数列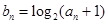 ,求数列
,求数列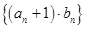 的前
的前 项和
项和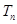 .
.