题目内容
已知数列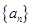 各项为非负实数,前n项和为
各项为非负实数,前n项和为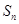 ,且
,且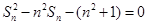
(1)求数列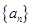 的通项公式;
的通项公式;
(2)当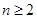 时,求
时,求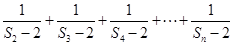 .
.
(1)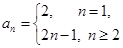 ;(2)原式
;(2)原式 .
.
解析试题分析:(1)将给出的等式分解因式可得 ,然后利用数列中
,然后利用数列中 和
和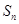 的关系求出
的关系求出 ,注意要验证当
,注意要验证当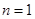 时
时 是否满足,若满足通项写出一个式子,若不满足须写出分段函数的形式;(2)由(1)已经求出
是否满足,若满足通项写出一个式子,若不满足须写出分段函数的形式;(2)由(1)已经求出 ,带入所求式子后裂项求和即可.
,带入所求式子后裂项求和即可.
试题解析:(1)∵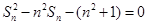

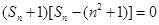
又∵数列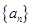 各项为非负实数 ∴
各项为非负实数 ∴
∴当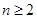 时
时 
当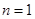 时
时 
故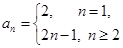 .
.
(2)当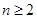 时
时 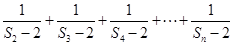


 .
.
考点:利用 和
和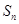 的关系求
的关系求 、裂项求和法.
、裂项求和法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
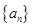 是正数组成的数列,
是正数组成的数列,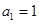 ,且点
,且点 在函数
在函数 的图象上.
的图象上. 满足
满足 ,
, ,求证:
,求证:
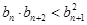 .
. 是首项为
是首项为 ,公差为
,公差为 的等差数列
的等差数列 ,
, 是其前
是其前 项和.
项和. ,
, ,求数列
,求数列 ,
,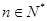 ,且
,且 、
、 、
、 成等比数列,证明:
成等比数列,证明: .
.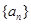 的前
的前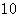 项和
项和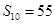 ,且
,且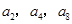 成等比数列.
成等比数列.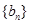 满足
满足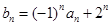 ,求
,求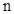 项和
项和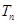 .
.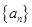 的通项公式为
的通项公式为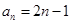 ,数列
,数列 的前
的前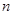 项和为
项和为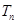 ,且满足
,且满足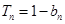 .
.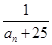 是
是 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 ,记
,记 .
.  ,
, 的值;
的值; 的通项公式;
的通项公式; 求证:对任意
求证:对任意 .
. 的前
的前 项和为
项和为 ,满足
,满足 且
且 构成等比数列.
构成等比数列. ;
; .
.