题目内容
设函数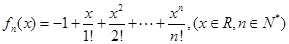
(Ⅰ)证明对每一个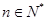 ,存在唯一的
,存在唯一的 ,满足
,满足 ;
;
(Ⅱ)由(Ⅰ)中的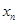 构成数列
构成数列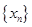 ,判断数列
,判断数列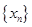 的单调性并证明;
的单调性并证明;
(Ⅲ)对任意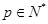 ,
,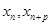 满足(Ⅰ),试比较
满足(Ⅰ),试比较 与
与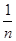 的大小.
的大小.
(Ⅰ)详见解析;(Ⅱ)数列 单调递减,证明详见解析;(Ⅲ)
单调递减,证明详见解析;(Ⅲ) .
.
解析试题分析:(Ⅰ)证明对每一个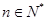 ,存在唯一的
,存在唯一的 ,满足
,满足 ,只需证明两点,第一证
,只需证明两点,第一证 在
在 上为单调函数,第二证,
上为单调函数,第二证, 在区间
在区间 的端点的函数值异号,本题是高次函数,可用导数法判断单调性,而判断
的端点的函数值异号,本题是高次函数,可用导数法判断单调性,而判断 的符号是,可用放缩法;(Ⅱ)由(Ⅰ)中的
的符号是,可用放缩法;(Ⅱ)由(Ⅰ)中的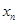 构成数列
构成数列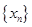 ,判断数列
,判断数列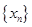 的单调性,由(Ⅰ)知
的单调性,由(Ⅰ)知 在
在 上递增,只需比较
上递增,只需比较 的大小,由(Ⅰ)知
的大小,由(Ⅰ)知 ,故
,故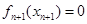 ,而
,而 ,从而得到
,从而得到 ,而
,而 ,所以
,所以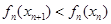 ,这样就可判断数列
,这样就可判断数列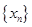 的单调性;(Ⅲ)对任意
的单调性;(Ⅲ)对任意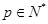 ,
,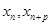 满足(Ⅰ),试比较
满足(Ⅰ),试比较 与
与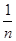 的大小,由(Ⅱ)知数列
的大小,由(Ⅱ)知数列 单调递减,故
单调递减,故 ,即比较
,即比较 与
与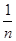 的大小,由(Ⅰ)知
的大小,由(Ⅰ)知 ,写出
,写出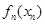 与
与 的式子,两式作差即可.本题函数与数列结合出题,体现学科知识交汇点的灵活运用,的确是一个好题,起到把关题的作用.
的式子,两式作差即可.本题函数与数列结合出题,体现学科知识交汇点的灵活运用,的确是一个好题,起到把关题的作用.
试题解析:(Ⅰ) ,显然,当
,显然,当 时,
时, ,故
,故 在
在 上递增,又
上递增,又 ,
, ,故存在唯一的
,故存在唯一的 ,满足
,满足 ;
;
(Ⅱ)因为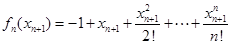 ,所以
,所以 ,
, ,由(Ⅰ)知
,由(Ⅰ)知 在
在 上递增,故
上递增,故 ,即数列
,即数列 单调递减;
单调递减;
(Ⅲ) 由(Ⅱ)数列 单调递减,故
单调递减,故 ,而
,而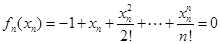 ,
, ,两式相减:并结合
,两式相减:并结合 ,以及
,以及 ,
,

 ,所以有
,所以有 .
.
考点:函数与导数,导数与函数的单调性、根的存在性定理,数列的单调性,不等式中的放缩法的运用,学生的基本推理能力,及基本运算能力以及转化与化归的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
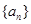 的前3项和
的前3项和 =9,且
=9,且 成等比数列
成等比数列 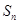 ;
; 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值
的最小值 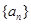 的前
的前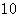 项和
项和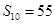 ,且
,且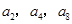 成等比数列.
成等比数列.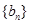 满足
满足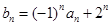 ,求
,求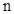 项和
项和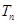 .
. 满足
满足 ,
,
 ,求数列
,求数列 的前
的前 项和
项和 .
. 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 ,记
,记 .
.  ,
, 的值;
的值; 的通项公式;
的通项公式; 求证:对任意
求证:对任意 .
. 中,
中, ,前
,前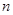 和
和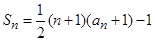
 的前
的前 ,是否存在实数
,是否存在实数 ,使得
,使得 对一切正整数
对一切正整数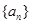 满足:
满足: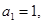 点
点 均在直线
均在直线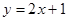 上.
上.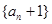 为等比数列,并求出数列
为等比数列,并求出数列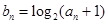 ,求数列
,求数列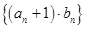 的前
的前 项和
项和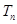 .
. ,
, ,
, ,记
,记
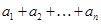 ,
,
 ,
,
 (
( ),若对于任意
),若对于任意 ,
, ,
, 成等差数列.
成等差数列. 的前
的前 项和.
项和.