Question

7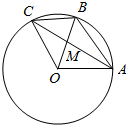．如图，A，B是单位圆上的相异两定点（O为圆心），且∠AOB=θ（θ为锐角）．点C为单位圆上的动点，线段AC交线段OB于点M．
（1）求$\overrightarrow{OA}•\overrightarrow{AB}$（结果用θ表示）；
（2）若θ=60°
①求$\overrightarrow{CA}•\overrightarrow{CB}$的取值范围；
②设$\overrightarrow{OM}=t\overrightarrow{OB}$（0＜t＜1），记$\frac{{{S_{△COM}}}}{{{S_{△BMA}}}}$=f（t），求函数f（t）的值域．

Answer 1

分析 （1）直接利用平面向量的数量积把$\overrightarrow{OA}•\overrightarrow{AB}$用θ表示；
（2）①利用向量的数量积运算结合向量的加减法运算把$\overrightarrow{CA}•\overrightarrow{CB}$用∠BOC表示，化简整理后由∠BOC得范围求得$\overrightarrow{CA}•\overrightarrow{CB}$的取值范围；
②设$\overrightarrow{AM}=λ\overrightarrow{AC}（0＜λ＜1）$，则$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM}=\overrightarrow{OA}+λ\overrightarrow{AC}=（1-λ）\overrightarrow{OA}+λ\overrightarrow{OC}=t\overrightarrow{OB}$，∴$\overrightarrow{OC}=\frac{t}{λ}\overrightarrow{OB}-\frac{1-λ}{λ}\overrightarrow{OA}$，由$\overrightarrow{OC}=1$可得，$|\frac{t}{λ}\overrightarrow{OB}-\frac{1-λ}{λ}\overrightarrow{OA}|=1$，整理得$λ=\frac{{{t^2}-t+1}}{2-t}$，然后把$\frac{{{S_{△COM}}}}{{{S_{△BMA}}}}$转化为含有t的代数式，换元后借助于函数单调性求得函数f（t）的值域．

解答 解：（1）$\overrightarrow{OA}•\overrightarrow{AB}=|\overrightarrow{OA}||\overrightarrow{AB}|cos（π-∠OAB）$=$-|\overrightarrow{AB}|cos∠OAB=-2{sin^2}\frac{θ}{2}$；
（2）当θ=60°时，$\overrightarrow{OA}•\overrightarrow{OB}=\frac{1}{2}$
①$\overrightarrow{CA}•\overrightarrow{CB}=（\overrightarrow{OA}-\overrightarrow{OC}）•（\overrightarrow{OB}-\overrightarrow{OC}）$=$\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OA}•\overrightarrow{OC}-\overrightarrow{OC}•\overrightarrow{OB}+1$．
设∠BOC=α，由条件知，$α∈[0，\frac{2π}{3}]$，
∴$\overrightarrow{CA}•\overrightarrow{CB}=\frac{3}{2}-cos（\frac{π}{3}+α）-cosα=\frac{3}{2}-\frac{1}{2}cosα+\frac{{\sqrt{3}}}{2}sinα-cosα$
=$\frac{3}{2}-\frac{3}{2}cosα+\frac{{\sqrt{3}}}{2}sinα=\frac{3}{2}-\sqrt{3}（\frac{{\sqrt{3}}}{2}cosα-\frac{1}{2}sinα）$=$\frac{3}{2}-\sqrt{3}cos（α+\frac{π}{6}）$．
∵$α∈[0，\frac{2π}{3}]$，∴$cos（α+\frac{π}{6}）∈[-\frac{{\sqrt{3}}}{2}，\frac{{\sqrt{3}}}{2}]$，
∴$\overrightarrow{CA}•\overrightarrow{CB}$∈[0，3]；
②设$\overrightarrow{AM}=λ\overrightarrow{AC}（0＜λ＜1）$，则$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM}=\overrightarrow{OA}+λ\overrightarrow{AC}=（1-λ）\overrightarrow{OA}+λ\overrightarrow{OC}=t\overrightarrow{OB}$，
∴$\overrightarrow{OC}=\frac{t}{λ}\overrightarrow{OB}-\frac{1-λ}{λ}\overrightarrow{OA}$，
由$\overrightarrow{OC}=1$可得，$|\frac{t}{λ}\overrightarrow{OB}-\frac{1-λ}{λ}\overrightarrow{OA}|=1$，
即${（\frac{t}{λ}）^2}+{（\frac{1-λ}{λ}）^2}-2×\frac{t}{λ}×\frac{1-λ}{λ}×\overrightarrow{OA}•\overrightarrow{OB}=1$，整理得$λ=\frac{{{t^2}-t+1}}{2-t}$，
∴$\frac{CM}{AM}=\frac{1-λ}{λ}=\frac{{1-{t^2}}}{{{t^2}-t+1}}$，
∴$\frac{{{S_{△COM}}}}{{{S_{△COM}}}}=\frac{{\overrightarrow{OM}•\overrightarrow{CM}}}{{\overrightarrow{MB}•\overrightarrow{AM}}}=\frac{t}{1-t}×\frac{{1-{t^2}}}{{{t^2}-t+1}}=\frac{{{t^2}+t}}{{{t^2}-t+1}}$．
即$f（t）=\frac{{{t^2}+t}}{{{t^2}-t+1}}（0＜t＜1）$．
而$f（t）=\frac{{t}^{2}+t}{{t}^{2}-t+1}=1+\frac{2t-1}{{t}^{2}-t+1}$．
令$2t-1=a（-1＜a＜1），g（a）=1+\frac{a}{{{{（\frac{a+1}{2}）}^2}-\frac{a+1}{2}+1}}=1+\frac{4a}{{{a^2}+3}}$，
当a=0时，g（0）=1；
当a≠0时，$g（a）=1\frac{4}{{a+\frac{3}{a}}}$，利用单调性定义可证明函数$y=a+\frac{3}{a}$在（-1，0）和（0，1）都是递减的，
因此，$a+\frac{3}{a}＞4$或$a+\frac{3}{a}＜-4$，
∴函数$f（t）=\frac{{{t^2}+t}}{{{t^2}-t+1}}（0＜t＜1）$值域是（0，2）．

点评 本题考查平面向量的数量积运算，考查了三角函数值域的求法，训练了利用配方法和函数单调性求函数的值域，考查学生的逻辑思维能力和运算能力，难度较大．