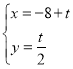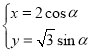题目内容
【题目】如图,四棱锥P﹣ABCD的底面ABCD为直角梯形,BC//AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD;点E、M分别为PD、PC的中点.
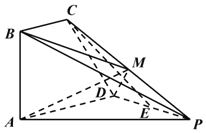
(1)证明:CE//平面PAB;
(2)求三棱锥M﹣BAD的体积;
(3)求直线DM与平面ABM所成角的正弦值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,利用三角形的中位线证得
,利用三角形的中位线证得![]() ,而
,而![]() ,由此证得
,由此证得![]() ,由此证得四边形
,由此证得四边形![]() 是平行四边形,进而证得
是平行四边形,进而证得![]() ,从而证得
,从而证得![]() 平面
平面![]() .
.
(2)根据等边三角形的性质,结合面面垂直的性质定理,求得![]() 到平面
到平面![]() 的距离,而
的距离,而![]() 是
是![]() 的中点,故
的中点,故![]() 到平面
到平面![]() 的距离是
的距离是![]() 到平面
到平面![]() 的距离的一半.由此求得
的距离的一半.由此求得![]() 到平面
到平面![]() 的距离,进而求得三棱锥
的距离,进而求得三棱锥![]() 的体积.
的体积.
(3)建立空间直角坐标系,利用直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,计算出线面角的正弦值.
的法向量,计算出线面角的正弦值.
(1)证明:设PA的中点为N,连结EN,BN,
∵E为PD中点,∴EN为△PAD的中位线,
∴EN//AD,且EN![]() AD,
AD,
在梯形ABCD中,BC//AD,且BC![]() AD,
AD,
∴BC//EN,且BC=EN,∴四边形ENBC是平行四边形,∴CE//BN,
∵BN平面PAB,CE平面PAB,∴CE//平面PAB.
(2)解:∵四棱锥P﹣ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,
∴![]() 1,
1,
∵△PAD为等边三角形,平面ABCD⊥平面PAD,点M是PC的中点.
设AD的中点为O,则PA=PD,∴PO⊥AD,
∴M到平面ABD的距离d![]() ,
,
∴三棱锥M﹣BAD的体积V![]() .
.
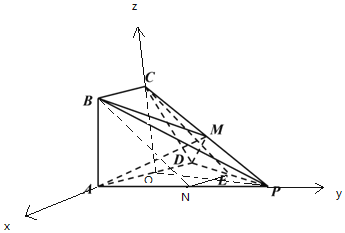
(3)∵平面PAD⊥平面ABCD,交线为AD,PO平面PAD,
∴PO⊥平面ABCD,
又∵CO//BA,∠BAD=90°,∴CO⊥AD,
∴OA,OC,OP,OC两两垂直,
以O为原点,OA,OC,OP,OC所在直线分别为x,y,z轴,建立空间直角坐标系,
则A(1,0,0),B(1,0,1),M(0,![]() ,
,![]() ),D(﹣1,0,0),
),D(﹣1,0,0),
![]() (0,0,1),
(0,0,1),![]() (﹣1,
(﹣1,![]() ,
,![]() ),
),
设平面ABM的法向量![]() (x,y,z),
(x,y,z),
则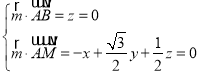 ,取x
,取x![]() ,得
,得![]() (
(![]() ),
),![]() (1,
(1,![]() ,
,![]() ),
),
cos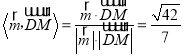 ,
,
∴直线DM与平面ABM所成角的正弦值为![]() .
.

 名校课堂系列答案
名校课堂系列答案