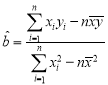题目内容
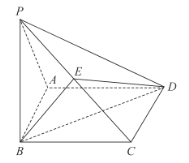
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() .
.
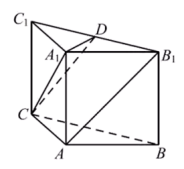
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() ,求几何体
,求几何体![]() 的体积.
的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ)2
【解析】
(Ⅰ)连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,证出
,证出![]() ,利用线面平行的判定定理即可证出.
,利用线面平行的判定定理即可证出.
(Ⅱ)根据题意可求出![]() ,在
,在![]() 中,利用余弦定理求出
中,利用余弦定理求出![]() ,由
,由![]() 结合三棱锥的体积公式即可求解.
结合三棱锥的体积公式即可求解.
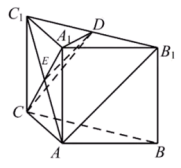
(Ⅰ)如图,连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,
因为在直三棱柱![]() 中,四边形
中,四边形![]() 是矩形,
是矩形,
所以点![]() 是
是![]() 的中点,
的中点,
因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)因为棱柱![]() 是直三棱柱,
是直三棱柱,
所以![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
因为异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
所以![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() .
.
根据余弦定理,在![]() 中,
中,![]() ,
,
可得![]() ,
,
因为![]() ,
,![]() ,所以由勾股定理可得
,所以由勾股定理可得![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,
,
所以![]()
![]()
![]() .
.
所以几何体![]() 的体积为2.
的体积为2.

练习册系列答案
相关题目
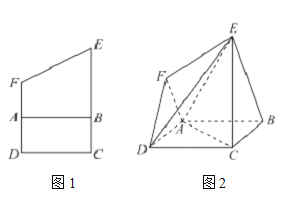
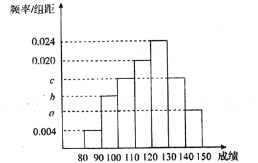
【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差数列且
.其中a,b,c成等差数列且![]() .物理成绩统计如表.(说明:数学满分150分,物理满分100分)
.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
(1)根据频率分布直方图,请估计数学成绩的平均分;
(2)根据物理成绩统计表,请估计物理成绩的中位数;
(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从数学成绩为“优”的同学中随机抽取2人,求两人恰好均为物理成绩“优”的概率.