题目内容
数列的前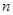 项的和
项的和 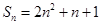 ,求数列的通项公式.
,求数列的通项公式.
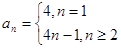
解析试题分析:当n=1时, ,当
,当 时,
时, ,求出
,求出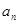 后,在验证
后,在验证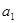 是否满足即可.
是否满足即可.
试题解析:当n=1时,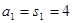 ,
,
当 时,
时, ,又
,又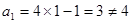 ,所以
,所以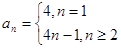 .
.
考点: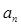 与
与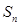 的关系
的关系

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
题目内容
数列的前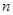 项的和
项的和 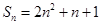 ,求数列的通项公式.
,求数列的通项公式.
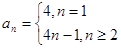
解析试题分析:当n=1时, ,当
,当 时,
时, ,求出
,求出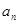 后,在验证
后,在验证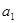 是否满足即可.
是否满足即可.
试题解析:当n=1时,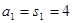 ,
,
当 时,
时, ,又
,又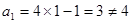 ,所以
,所以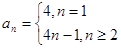 .
.
考点: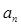 与
与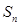 的关系
的关系

 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案