题目内容
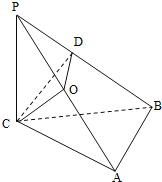
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.

(1)求证:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
( 1)由题设条件,易证得PC⊥AB,CD⊥AB,故可由线面垂直的判定定理证得AB⊥平面PCB;(2)由图形知,取AP的中点O,连接CO、DO,可证得∠COD为二面角C﹣PA﹣B的平面角,在△CDO中求∠COD即可.
(1)证明:∵PC⊥平面ABC,AB平面ABC,
∴PC⊥AB.
∵CD⊥平面PAB,AB平面PAB,
∴CD⊥AB.又PC∩CD=C,∴AB⊥平面PCB.
(2)取AP的中点O,连接CO、DO.
∵PC=AC=2,∴CO⊥PA,CO![]() ,
,
∵CD⊥平面PAB,由三垂线定理的逆定理,得DO⊥PA.
∴∠COD为二面角C﹣PA﹣B的平面角.
由(1)AB⊥平面PCB,∴AB⊥BC,
又∵AB=BC,AC=2,求得BC![]()
PB![]() ,CD
,CD![]()
∴![]()
cos∠COD![]() .
.

练习册系列答案
相关题目