题目内容
【题目】![]() 统计学中将
统计学中将![]() 个数
个数![]() 的和记作
的和记作![]()
(1)设![]()
![]() ,求
,求![]() ;
;
(2)是否存在互不相等的非负整数![]() ,
,![]() ,使得
,使得![]() 成立,若存在,请写出推理的过程;若不存在请证明;
成立,若存在,请写出推理的过程;若不存在请证明;
(3)设![]()
![]() 是不同的正实数,
是不同的正实数,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,判断
,判断![]() 是否为一个等比数列,请说明理由.
是否为一个等比数列,请说明理由.
【答案】(1)79;(2)不存在,证明详见解析;(3)是等比数列,理由详见解析.
【解析】
(1)代值计算结果.(2)距离2019最近的2的幂次为![]() ,而2019小于2048,所以
,而2019小于2048,所以![]() ,但是2048和2019的差不大,所以可以研究他们的差如何表示.(3)利用数学归纳法证明.
,但是2048和2019的差不大,所以可以研究他们的差如何表示.(3)利用数学归纳法证明.
(1)因为![]() ,所以
,所以![]()
所以![]()
(2)因为![]() ,
,![]()
又![]() ,所以
,所以![]() 中最大可能是10,
中最大可能是10,
因为![]() ,
,
![]()
所以![]()
又![]() ,
,
所以必有![]() ·
·
又因为![]() ,所以
,所以![]()
所以必然存在某几项![]() ,其中
,其中![]() ,
,
只有![]() ,
,
所以存在这样互不相等的非负整数![]() ,
,![]() ,
,
使得![]() 成立。
成立。
(3)数学归纳法证明:
当![]() ,代入
,代入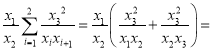
![]() ,
,
化简得![]() 所以
所以![]() 成等比数列
成等比数列
假设当![]() 时
时![]() 成等比数列,
成等比数列,![]() 是不同的正实数
是不同的正实数
记![]() ,设
,设![]()
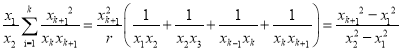
化简整理得:
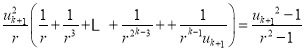
去分母同乘以![]() 得
得
![]()
整理![]()
![]()
因为![]()
得![]() ,从而
,从而![]() ,
,
所以![]() 时
时![]() 是等比数列
是等比数列

练习册系列答案
相关题目