题目内容
【题目】若存在![]() 与正实数
与正实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 在
在![]() 处存在距离为
处存在距离为![]() 的对称点,把具有这一性质的函数
的对称点,把具有这一性质的函数![]() 称之为“
称之为“![]() 型函数”.
型函数”.
(1)设![]() ,试问
,试问![]() 是否是“
是否是“![]() 型函数”?若是,求出实数
型函数”?若是,求出实数![]() 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(2)设![]() 对于任意
对于任意![]() 都是“
都是“![]() 型函数”,求实数
型函数”,求实数![]() 的取值范围.
的取值范围.
【答案】(1)是,![]() ;(2)
;(2)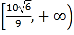 .
.
【解析】
(1)假设函数![]() 是“
是“![]() 型函数”,由定义得出
型函数”,由定义得出![]() ,经过化简计算出正实数
,经过化简计算出正实数![]() 的值即可;
的值即可;
(2)由题中定义得出![]() ,利用参变量分离法得出
,利用参变量分离法得出![]() ,利用双勾函数的单调性求出
,利用双勾函数的单调性求出![]() 在
在![]() 上的值域,即可得出实数
上的值域,即可得出实数![]() 的取值范围.
的取值范围.
(1)假设函数![]() 是“
是“![]() 型函数”,由定义得出
型函数”,由定义得出![]() ,
,
![]() ,由
,由![]() ,得
,得![]() ,
,
则有![]() ,
,![]() ,化简得
,化简得![]() ,解得
,解得![]() .
.
因此,函数![]() 是“
是“![]() 型函数”;
型函数”;
(2)![]() 对于任意
对于任意![]() 都是“
都是“![]() 型函数”,
型函数”,
则![]() ,
,
即![]() ,
,
化简得![]() ,即
,即![]() ,
,
由双勾函数的单调性可知,函数![]() 在
在![]() 上是增函数.
上是增函数.
当![]() 时,
时,![]() ,所以,
,所以,![]() ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是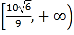 .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目