题目内容
【题目】已知p:-x2-2x+8≥0,q:x2-2x+1-m2≤0(m>0).
(1)若p是q的充分条件,求实数m的取值范围;
(2)若“¬p”是“¬q”的充分条件,求实数m的取值范围.
【答案】(1)![]() ;(2)0<m≤1.
;(2)0<m≤1.
【解析】
(1)解出关于p,q的不等式,根据若p是q的充分条件,得到[-4,2][1-m,1+m],求出m的范围即可;
(2)根据“¬p”是“¬q”的充分条件,可推出q是p的充分条件,得到[1-m,1+m][-4,2],求出m的范围即可.
(1)p:-x2-2x+8≥0,q:x2-2x+1-m2≤0(m>0).
故p:-4≤x≤2,q:1-m≤x≤1+m,
若p是q的充分条件,
则[-4,2][1-m,1+m],
故![]() ,
,
解得:![]() ;
;
(2)若“¬p”是“¬q”的充分条件,
即q是p的充分条件,
则[1-m,1+m][-4,2],
∴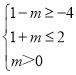 ,
,
解得:0<m≤1.

练习册系列答案
相关题目
【题目】我校对高二600名学生进行了一次知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
分 组 | 频 数 | 频 率 |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 |
|
[80,90) |
|
|
[90,100] | 14 | 0.28 |
合 计 |
| 1.00 |
(1)填写频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)请你估算该年级学生成绩的中位数;
(3)如果用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,再从6人中选2人,求2人分数都在[80,90)的概率.