题目内容
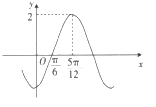
【题目】大学生王某开网店创业专卖某种文具,他将这种文具以每件2元的价格售出,开始第一个月就达到1万件,此后每个月都比前一个月多售出1.5万件,持续至第10个月,在第11个月出现下降,第11个月出售了13万件,第12个月出售了9万件,第13个月出售了7万件,另据观察,第18个月销量仍比上个月低,而他前十个月每月投入的成本与月份的平方成正比,第4个月成本为8000元,但第11个月起每月成本固定为3万元,现打算用函数![]() (
(![]() )或
)或![]() (
(![]() ,
,![]() ,
,![]() )来模拟销量下降期间的月销量.
)来模拟销量下降期间的月销量.
(1)请判断销量下降期间采用哪个函数模型来模拟销量函数更合理,并写出前20个月销量与月份![]() 之间的函数关系式;
之间的函数关系式;
(2)前20个月内,该网店取得的月利润的最高纪录是多少,出现在哪个月?
【答案】(1)![]() 更合理,
更合理, ;(2)24万,第10个月
;(2)24万,第10个月
【解析】
(1)分别采用待定系数法,算出![]() 和
和![]() 表达式,再检验
表达式,再检验![]() 时是否符合题设即可
时是否符合题设即可
(2)列出利润![]() 关于
关于![]() 的表达式,根据函数性质分别计算两分段函数的利润最大值,即可求解
的表达式,根据函数性质分别计算两分段函数的利润最大值,即可求解
(1)假设从第11个月开始,月销量符合![]() 的变化趋势,则
的变化趋势,则![]() 均在
均在![]() 上,即
上,即 ,
,![]() ,对称轴为
,对称轴为![]() ,当
,当![]() 时,不符合题意,故此模型舍去;
时,不符合题意,故此模型舍去;
假设从第11个月开始,月销量符合![]() 的变化趋势,则
的变化趋势,则![]() 均在
均在![]() 上,即
上,即 ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
故![]() 更合理,此时
更合理,此时![]() ,
,![]() ;
;
由题知前10个月符合一次函数模型,设![]() ,将
,将![]() 代入,解得
代入,解得![]() ,则
,则![]() ,
,![]() ,故
,故 
(2)设前10个月成本(万元)与月份的关系为![]() ,将
,将![]() 代入解得
代入解得![]() ,则
,则![]() ,前10个月利润可表示为
,前10个月利润可表示为![]() ,当
,当![]() 时取到最大值,
时取到最大值,![]() ;当
;当![]() 时,
时,![]() 单调递减,第11个月利润有最大值,
单调递减,第11个月利润有最大值,
![]() ;
;
故月利润最高记录为24万元,出现在第10个月.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.