��Ŀ����
����Ŀ����У�Ը߶�600��ѧ��������һ��֪ʶ����,�����г�ȡ�˲���ѧ���ijɼ�(����100��)��Ϊ����,������������δ��ɵ�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ.
������ | Ƶ���� | Ƶ���� |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | �� |
[80,90) | �� | �� |
[90,100] | 14 | 0.28 |
������ | �� | 1.00 |
(1)��дƵ�ʷֲ����еĿո�,��ȫƵ�ʷֲ�ֱ��ͼ,�����ÿ��С���ζ�Ӧ����������;
(2)���������꼶ѧ���ɼ�����λ��;
(3)����÷ֲ�����ķ���������������[60,70)��[80,90)�����й���ȡ6��,�ٴ�6����ѡ2��,��2�˷�������[80,90)�ĸ���.

���𰸡�(1)�𰸼�������(2)83.125��(3) ![]()
�����������������
(1)������ⲹȫƵ�ʷֲ�����Ȼ�����Ƶ�ʷֲ�ֱ��ͼ���ɣ�
(2)����λ��Ϊx,������λ���������Ϊ0.5�з��̿ɵ���λ��ԼΪ83.125.
(3)������ɵó�ȡ�ķ�����[60,70)��[80,90)�������ֱ�Ϊ2�˺�4��.����ѳ�ȡ��6������ѡ���˵����п��ܽ����15��,2�˷�������[80,90)���¼���6��,��Ϲŵ���ͼ��㹫ʽ�ɵ���������ĸ���ֵΪ![]() .
.
���������
(1)��дƵ�ʷֲ����еĿո�,���±�:
������ | Ƶ���� | Ƶ���� |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | 0.2 |
[80,90) | 16 | 0.32 |
[90,100] | 14 | 0.28 |
������ | 50 | 1.00 |
��ȫƵ�ʷֲ�ֱ��ͼ,����ͼ:
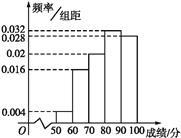
(2)����λ��Ϊx,�������0.04+0.16+0.2+0.032��(x-80)=0.5,
���x=83.125,������λ��ԼΪ83.125.
(3)������֪����������[60,70)��8��,����������[80,90)��16��,
�÷ֲ�����ķ���������������[60,70)��[80,90)�����й���ȡ6��,
���ȡ�ķ�����[60,70)��[80,90)�������ֱ�Ϊ2�˺�4��.
�Ƿ�����[60,70)��Ϊa1,a2,��[80,90)��Ϊb1,b2,b3,b4.
���ѳ�ȡ��6������ѡ���˵����п��ܽ����15��,�ֱ�Ϊ{a1,a2},{a1,b1},{a1,b2},{a1,b3},{a1,b4},{a2,b1},{a2,b2},{a2,b3},{a2,b4},{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4},
����2�˷�������[80,90)��Ϊ�¼�A,
���¼�A����{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4}��6��,����P(A)= ![]() .
.

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�����Ŀ�����Ź�������ˮƽ����ߣ����ó������ε���Խ��Խ�࣬�乫˾ͳ����2012��2016������䱾��˾ְ��ÿ�괺���ڼ�������εļ�ͥ��������ͳ�����������ʾ��
���x | 2012 | 2013 | 2014 | 2015 | 2016 |
��ͥ��y | 6 | 10 | 16 | 22 | 26 |
��1�������������ݣ���������ڼ�������εļ�ͥ�������֮��Ļع�ֱ�߷���y=bx+a���ж�����֮���Ƿ�������ػ��Ǹ���أ�
��2�����������ֱ�߷��̹��Ƹù�˾2019�괺���ڼ���������εļ�ͥ����

