题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{sin\frac{πx}{2}(x≤0)}\\{f(x-2)+2(x>0)}\end{array}\right.$,把方程f(x)-x=0的实数解按从小到大的顺序排列成一个数列$\left\{{a_n}\right\}(n∈{N^*})$,设$h(x)=x+{log_2}\frac{2+x}{8-x}$,则数列{h(an)}的各项之和为( )| A. | 36 | B. | 33 | C. | 30 | D. | 27 |
分析 方程f(x)-x=0的实数解可化为函数f(x)与函数y=x的交点的横坐标,作函数f(x)与函数y=x的图象,结合图象及$h(x)=x+{log_2}\frac{2+x}{8-x}$的定义域可得数列{h(an)}中an仅可以取-1,0,1,2,3,4,5,6,7;又由h(x)+h(6-x)=$(x+{log_2}\frac{2+x}{8-x})$$+(6-x+{log_2}\frac{8-x}{2+x})$=6,从而解得.
解答 解:方程f(x)-x=0的实数解可化为函数f(x)与函数y=x的交点的横坐标,
作函数f(x)与函数y=x的图象如下,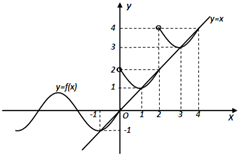
结合图象可得,
an=n-2;
又∵$h(x)=x+{log_2}\frac{2+x}{8-x}$的定义域为(-2,8),
∴数列{h(an)}中an仅可以取-1,0,1,2,3,4,5,6,7;
又∵h(x)+h(6-x)=$(x+{log_2}\frac{2+x}{8-x})$$+(6-x+{log_2}\frac{8-x}{2+x})$=6,
且$h(3)=3+{log_2}\frac{2+3}{8-3}=3$,
∴h(-1)+h(0)+h(1)+h(2)+h(3)+h(4)+h(5)+h(6)+h(7)
=(h(-1)+h(7))+(h(0)+h(6))+(h(1)+h(5))+(h(2)+h(4))+h(3)
=6×4+3=27.
故选:D.
点评 本题考查了数形结合的思想应用,同时考查了函数与数列的综合应用,属于难题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
6.将函数f(x)=sin(2x-$\frac{π}{3}$)的图象上各点的横坐标压缩到原来的$\frac{1}{2}$,再将图象向左平移$\frac{π}{3}$个单位,那么所得到的图象的解析表达式为( )
| A. | y=sin(4x+$\frac{π}{3}$) | B. | y=sin(x-$\frac{2π}{3}$) | C. | y=sin4x | D. | y=-sin4x |
4.已知点M(x,y)满足$\left\{\begin{array}{l}x≥1\\ x-y+1≥0\\ 2x-y-2≤0.\end{array}\right.$若ax+y的最小值为3,则a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.已知a、b为异面直线,若c∥a,则c与b的位置关系是( )
| A. | 相交 | B. | 异面 | C. | 平行 | D. | 相交或异面. |
6.在△ABC中,a2-b2-c2-bc=0,则A等于( )
| A. | 60° | B. | 45° | C. | 120° | D. | 30° |