题目内容
((本小题满分12分)
在边长为5的菱形ABCD中,AC=8。现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为
(I)求证:平面ABD⊥平面CBD;
(II)若M是AB的中点,求折起后AC与平面MCD所成角的一个三角函数值.
在边长为5的菱形ABCD中,AC=8。现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为

(I)求证:平面ABD⊥平面CBD;
(II)若M是AB的中点,求折起后AC与平面MCD所成角的一个三角函数值.
(Ⅰ)证明:菱形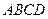 中,记
中,记 交点为
交点为 ,
,  ,
,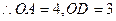
翻折后变成三棱椎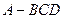 ,在△
,在△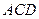 中,
中,
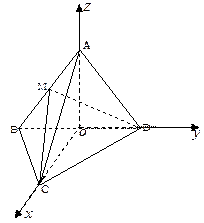

=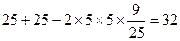
在△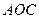 中,
中,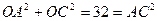 ,
,
∴∠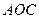 =90°,即
=90°,即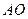 ⊥
⊥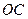 ,又
,又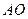 ⊥
⊥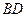 ,
,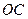 ∩
∩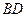 =
=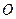 ,
,
∴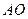 ⊥平面
⊥平面 , ………………………4分
, ………………………4分
又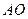
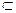 平面
平面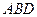 ,∴平面
,∴平面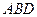 ⊥平面
⊥平面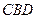 .
.
(Ⅱ)解:由(Ⅰ)知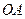 ,
,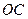 ,
,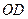 两两互相垂直,分别以
两两互相垂直,分别以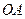 ,
,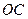 ,
, 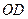 所在直线为坐标轴建系,
所在直线为坐标轴建系,
则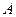 (0,0,4),
(0,0,4),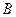 (0,-3,0),
(0,-3,0),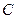 (4,0,0) ,
(4,0,0) ,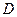 (0,3,0) ,
(0,3,0) ,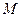 (0,-
(0,-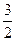 ,2),
,2),
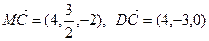 ,
,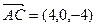 ,…………………………………8分
,…………………………………8分
设平面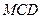 的一个法向量为
的一个法向量为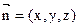 ,则由
,则由
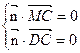 ,得
,得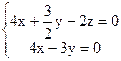 ,…10分 令y=4,有
,…10分 令y=4,有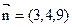 ……10分
……10分
设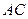 与平面
与平面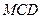 所成角为θ,
所成角为θ,
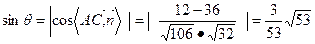
∴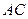 与平面
与平面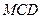 所成角的正弦值为
所成角的正弦值为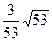 , …………………………………12分
, …………………………………12分
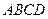 中,记
中,记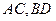 交点为
交点为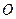 ,
,  ,
,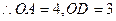
翻折后变成三棱椎
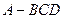 ,在△
,在△ 中,
中,

=
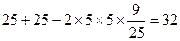
在△
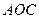 中,
中,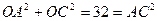 ,
,∴∠
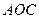 =90°,即
=90°,即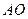 ⊥
⊥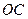 ,又
,又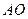 ⊥
⊥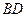 ,
,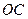 ∩
∩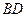 =
=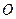 ,
,∴
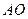 ⊥平面
⊥平面 , ………………………4分
, ………………………4分又
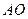
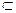 平面
平面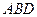 ,∴平面
,∴平面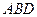 ⊥平面
⊥平面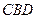 .
. (Ⅱ)解:由(Ⅰ)知
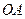 ,
,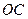 ,
,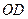 两两互相垂直,分别以
两两互相垂直,分别以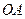 ,
,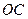 ,
, 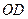 所在直线为坐标轴建系,
所在直线为坐标轴建系,则
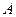 (0,0,4),
(0,0,4),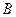 (0,-3,0),
(0,-3,0),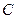 (4,0,0) ,
(4,0,0) ,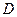 (0,3,0) ,
(0,3,0) ,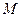 (0,-
(0,-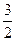 ,2),
,2),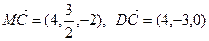 ,
,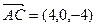 ,…………………………………8分
,…………………………………8分设平面
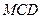 的一个法向量为
的一个法向量为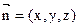 ,则由
,则由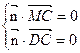 ,得
,得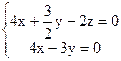 ,…10分 令y=4,有
,…10分 令y=4,有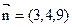 ……10分
……10分设
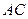 与平面
与平面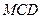 所成角为θ,
所成角为θ,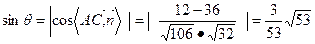
∴
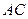 与平面
与平面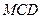 所成角的正弦值为
所成角的正弦值为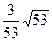 , …………………………………12分
, …………………………………12分略

练习册系列答案
相关题目
 平面ACE。
平面ACE。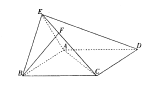
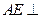 平面BCE;
平面BCE; 面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=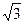 ,设D为
,设D为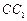 中点,
中点,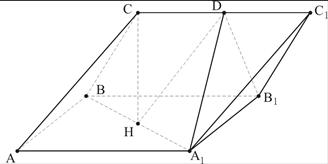
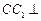 平面
平面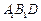 ;
;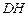 与平面
与平面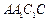 所成角的正弦值.
所成角的正弦值.
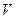 .
.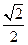 AB,∠ABC=60°,E为AB的中点.
AB,∠ABC=60°,E为AB的中点. 
 的底面为矩形,
的底面为矩形, 且
且 平面
平面 分别为
分别为 的中点.
的中点.
 ;
; 的大小值.
的大小值.
 中,已知点
中,已知点 、
、 、
、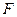 分别为棱
分别为棱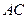 、
、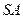 、
、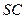 的中点.
的中点.
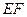 ∥平面
∥平面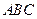 ;
; )若
)若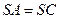 ,
,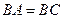 ,求证:
,求证: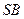 .
.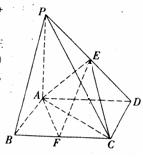
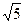 ,PD
,PD =4
=4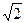 ,E是PD的中点
,E是PD的中点