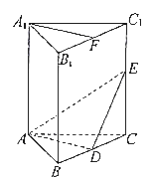
题目内容
【题目】若函数![]() 在其定义域上恰有两个零点,则正实数a的值为_____.
在其定义域上恰有两个零点,则正实数a的值为_____.
【答案】![]()
【解析】
当x≤0时,f(x)=x+2x,单调递增,由f(﹣1)f(0)<0,可得f(x)在(﹣1,0)有且只有一个零点;x>0时,f(x)=ax﹣lnx有且只有一个零点,即有a![]() 有且只有一个实根.令g(x)
有且只有一个实根.令g(x)![]() ,求出导数,求得单调区间,极值,即可得到a的值.
,求出导数,求得单调区间,极值,即可得到a的值.
当x≤0时,f(x)=x+2x,单调递增,
f(﹣1)=﹣1+2﹣1<0,f(0)=1>0,
由零点存在定理,可得f(x)在(﹣1,0)有且只有一个零点;
则由题意可得x>0时,f(x)=ax﹣lnx有且只有一个零点,
即有a![]() 有且只有一个实根.
有且只有一个实根.
令g(x)![]() ,g′(x)
,g′(x)![]() ,
,
当x>e时,g′(x)<0,g(x)递减;
当0<x<e时,g′(x)>0,g(x)递增.
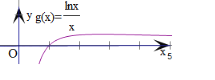
即有x=e处取得极大值,也为最大值,且为![]() ,当x
,当x![]()
如图g(x)的图象,当直线y=a(a>0)与g(x)的图象
只有一个交点时,则a![]() .
.
故答案为:![]() .
.

【题目】2019年4月,甲乙两校的学生参加了某考试机构举行的大联考,现从这两校参加考试的学生数学成绩在100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如下的茎叶图.
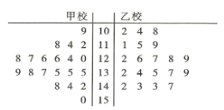
(1)试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数;
(2)若把数学成绩不低于135分的记作数学成绩优秀,根据茎叶图中的数据,判断是否有90![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关;
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关;
(3)若从这40名学生中选取数学成绩在![]() 的学生,用分层抽样的方式从甲乙两校中抽取5人,再从这5人中随机抽取3人分析其失分原因,求这3人中恰有2人是乙校学生的概率.
的学生,用分层抽样的方式从甲乙两校中抽取5人,再从这5人中随机抽取3人分析其失分原因,求这3人中恰有2人是乙校学生的概率.
参考公式与临界值表: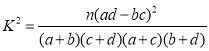 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某超市计划按月订购一种饮料,每天进货量相同,进货成本每瓶3元,售价每瓶5元,每天未售出的饮料最后打4折当天全部处理完![]() 根据往年销售经验,每天需求量与当天最高气温
根据往年销售经验,每天需求量与当天最高气温![]() 单位:
单位:![]() 有关
有关![]() 如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为100瓶
,需求量为300瓶;如果最高气温低于20,需求量为100瓶![]() 为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
![]() Ⅰ
Ⅰ![]() 求六月份这种饮料一天的需求量
求六月份这种饮料一天的需求量![]() 单位:瓶
单位:瓶![]() 的分布列,并求出期望EX;
的分布列,并求出期望EX;
![]() Ⅱ
Ⅱ![]() 设六月份一天销售这种饮料的利润为
设六月份一天销售这种饮料的利润为![]() 单位:元
单位:元![]() ,且六月份这种饮料一天的进货量为
,且六月份这种饮料一天的进货量为![]() 单位:瓶
单位:瓶![]() ,请判断Y的数学期望是否在
,请判断Y的数学期望是否在![]() 时取得最大值?
时取得最大值?