[题目]在正方体ABCDA1B1C1D1中.M为DD1的中点.O为四边形ABCD的中心.P为棱A1B1上任一点.则异面直线OP与MA所成的角为( )A.30°B.45°C.60°D.90° 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在正方体ABCDA1B1C1D1中，M为DD1的中点，O为四边形ABCD的中心，P为棱A1B1上任一点，则异面直线OP与MA所成的角为（）
A.30°
B.45°
C.60°
D.90°

【答案】D
【解析】解：∵A1B1⊥面ADD1A1 ， AM面ADD1A1 ， ∴A1B1⊥AM．
设点O与A1B1确定的平面为α，α∩AD=F且α∩BC=E，则F、E为AD、BC的中点，
根据正方形的性质，可得AM⊥A1F．
∵A1F∩A1B1=A1 ， A1F、A1B1平面面A1FEB1 ， ∴AM⊥面A1FEB1 ，
又∵OP面A1FEB1 ， ∴AM⊥OP．
即直线OP与直线AM所成的角是90°．
故选：D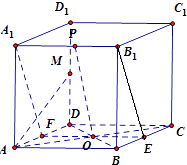

【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．

练习册系列答案

相关题目

【题目】已知函数

(Ⅰ)若有唯一解,求实数的值；

（Ⅱ）证明：当时，

（附：）

【题目】已知定义在R的函数f（x）= 是奇函数，其中a，b为实数
（1）求a，b的值
（2）用定义证明f（x）在R上是减函数
（3）若对于任意的t∈[﹣3，3]，不等式f（t2﹣2t）+f（﹣2t2+k）＜0恒成立，求k的取值范围．

【题目】已知函数的最大值为2.

（Ⅰ）求函数在上的单调递减区间；

（Ⅱ）中，角，，所对的边分别是，，，且，，若，求的面积.

【题目】下列结论正确的个数是（）
①命题“所有的四边形都是矩形”是特称命题；
②命题“x∈R，x2+2＜0”是全称命题；
③若p：x∈R，x2+4x+4≤0，则q：x∈R，x2+4x+4≤0是全称命题．
A.0
B.1
C.2
D.3

【题目】某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200度的部分按0.5元/度收费，超过200度但不超过400度的部分按0.8元/度收费，超过400度的部分按1.0元/度收费.

（1）求某户居民用电费用（单位：元）关于月用电量（单位：度）的函数解析式；

（2）为了了解居民的用电情况，通过抽样，获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年1月份用电费用不超过260元的点80%，求的值；

（3）在满足（2）的条件下，估计1月份该市居民用户平均用电费用（同一组中的数据用该组区间的中点值作代表）．

【题目】已知函数f（x）=alnx，g（x）=x2 ．其中x∈R．
（1）若曲线y=f（x）与y=g（x）在x=1处的切线相互平行，求两平行直线间的距离；
（2）若f（x）≤g（x）﹣1对任意x＞0恒成立，求实数a的值；
（3）当a＜0时，对于函数h（x）=f（x）﹣g（x）+1，记在h（x）图象上任取两点A、B连线的斜率为kAB ，若|kAB|≥1，求a的取值范围．

【题目】随机观测生产某种零件的某工厂25名工人的日加工零件数（单位：件），获得数据如下：
30，42，41，36，44，40，37，37，25，45，29，43，31，36，49，34，33，43，38，42，32，34，46，39，36．
根据上述数据得到样本的频率分布表如下：