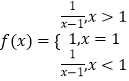题目内容
【题目】随机观测生产某种零件的某工厂25名工人的日加工零件数（单位：件），获得数据如下：
30，42，41，36，44，40，37，37，25，45，29，43，31，36，49，34，33，43，38，42，32，34，46，39，36．
根据上述数据得到样本的频率分布表如下：
分组 | 频数 | 频率 |
[25，30] | 3 | 0.12 |
（30，35] | 5 | 0.20 |
（35，40] | 8 | 0.32 |
（40，45] | n1 | f1 |
（45，50] | n2 | f2 |
（1）确定样本频率分布表中n1 ， n2 ， f1和f2的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）根据样本频率分布直方图，求在该厂任取4人，至少有1人的日加工零件数落在区间（30，35]的概率．
【答案】
（1）解：（40，45]的频数n1=7，频率f1=0.28；（45，50]的频数n2=2，频率f2=0.08；
（2）解：频率分布直方图：
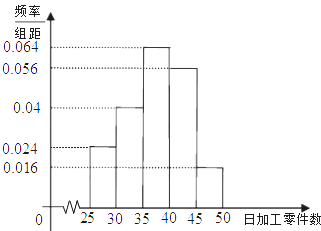
（3）解：设在该厂任取4人，没有一人的日加工零件数落在区间（30，35]为事件A，则至少有一人的日加工零件数落在区间（30，35]为事件，
已知该厂每人日加工零件数落在区间（30，35]的概率为 
= 
，
∴P（A）= 
=0.4096，
∴P（ 
）=1﹣P（A）=1﹣0，4096=0.5904，
∴在该厂任取4人，至少有1人的日加工零件数落在区间（30，35]的概率0.5904．
【解析】（1）利用所给数据，可得样本频率分布表中n1 ， n2 ， f1和f2的值；（2）根据上述频率分布表，可得样本频率分布直方图；（3）利用对立事件可求概率．
【考点精析】本题主要考查了频率分布直方图的相关知识点，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息才能正确解答此题．
