题目内容
已知直线y=kx-1与椭圆
+
=1相切,则k、a之间的关系式为( )
+=1相切,则k、a之间的关系式为( )| A．4a+4k2="1" | B．4k2-a=1 |
| C．a-4k2="1" | D．a+4k2=1 |
D
联立方程组得(a+4k2)x2-8kx+4-4a=0.
∵直线与椭圆相切,
∴Δ=(-8k)2-4(a+4k2)(4-4a)=0.
结合a>0得4k2+a-1=0.
∵直线与椭圆相切,
∴Δ=(-8k)2-4(a+4k2)(4-4a)=0.
结合a>0得4k2+a-1=0.
练习册系列答案
阅读快车系列答案
相关题目
+
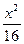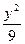=1的两焦点，经点F2的的直线交椭圆于点A、B，若|AB|=5，则|AF1|+|BF1|等于（ ）
=1(a>b>0)的左焦点F,A(-a,0)、B(0,b)是两个顶点.如果F到直线AB的距离等于
,那么椭圆的离心率为（ ）
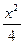+y2=1相交于A、B两点,当t变化时,|AB|的最大值为( )
C.
D.
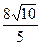
+y2=1(y≥0),求
的最大值、最小值.
-
=1表示焦点在y轴上的椭圆，那么实数a的取值范围是…( )