题目内容
(本小题满分13分)设数列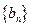 的前
的前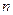 项和为
项和为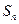 ,且
,且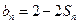 ;数列
;数列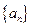 为等差数列,且
为等差数列,且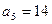 ,
,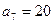 .(1)求数列
.(1)求数列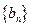 和
和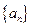 的通项公式;
的通项公式;
(2)若 ,
,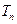 为数列
为数列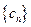 的前
的前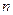 项和.求证:
项和.求证: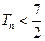 .
.
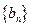 的前
的前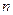 项和为
项和为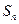 ,且
,且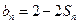 ;数列
;数列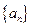 为等差数列,且
为等差数列,且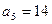 ,
,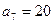 .(1)求数列
.(1)求数列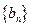 和
和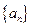 的通项公式;
的通项公式;(2)若
 ,
,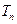 为数列
为数列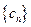 的前
的前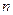 项和.求证:
项和.求证: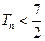 .
.(Ⅰ) 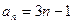 (Ⅱ)
(Ⅱ) 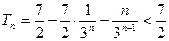
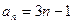 (Ⅱ)
(Ⅱ) 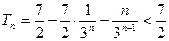
(1)由 ,令
,令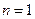 ,则
,则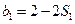 ,又
,又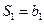 ,所以
,所以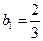 .…1分
.…1分
当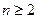 时,由
时,由 ,可得
,可得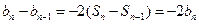 .即
.即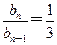 .…3分
.…3分
所以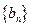 是以
是以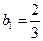 为首项,
为首项,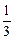 为公比的等比数列,于是
为公比的等比数列,于是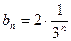 .………5分
.………5分
数列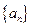 为等差数列,公差
为等差数列,公差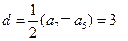 ,可得
,可得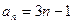 .…………7分
.…………7分
(2)从而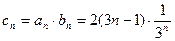 .
.
∴ …………10分
…………10分
∴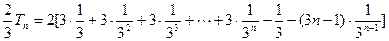 .
.
从而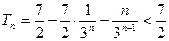 . …………………………………………13分
. …………………………………………13分
 ,令
,令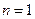 ,则
,则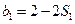 ,又
,又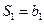 ,所以
,所以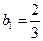 .…1分
.…1分当
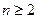 时,由
时,由 ,可得
,可得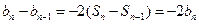 .即
.即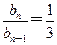 .…3分
.…3分所以
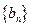 是以
是以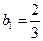 为首项,
为首项,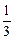 为公比的等比数列,于是
为公比的等比数列,于是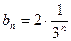 .………5分
.………5分数列
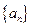 为等差数列,公差
为等差数列,公差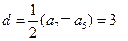 ,可得
,可得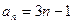 .…………7分
.…………7分(2)从而
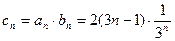 .
.∴
 …………10分
…………10分∴
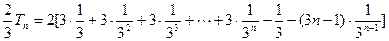 .
. 从而
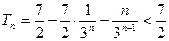 . …………………………………………13分
. …………………………………………13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
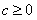 ,曲线
,曲线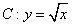 与直线
与直线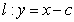 的交点为
的交点为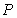 (异于原点
(异于原点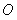 ),在曲线
),在曲线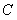 上取一点
上取一点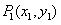 ,过点
,过点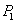 作
作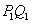 平行于
平行于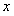 轴,交直线
轴,交直线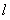 于点
于点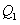 ,过点
,过点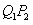 平行于
平行于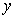 轴,交曲线
轴,交曲线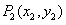 ,接着过点
,接着过点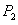 作
作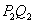 平行于
平行于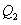 ,过点
,过点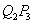 平行于
平行于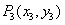 ,如此下去,可以得到点
,如此下去,可以得到点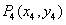 ,
,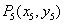 ,…,
,…,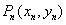 ,… . 设点
,… . 设点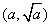 ,
,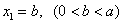 .
.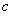 表示
表示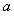 ,并证明
,并证明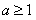 ;
; 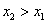 ,且
,且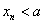 (
(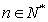 );
);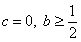 时,求证:
时,求证: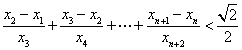 (
(
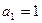 ,当
,当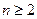 时,其前
时,其前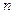 项和
项和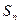 满足
满足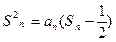
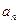 ;
;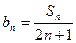 ,求数列{
,求数列{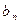 }的前项和
}的前项和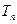
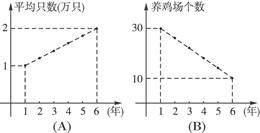
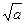 、
、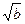 、
、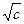 也成等差数列,则△ABC的形状为________________.
也成等差数列,则△ABC的形状为________________.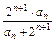 ,a1=2,求数列{an}的通项公式.
,a1=2,求数列{an}的通项公式.
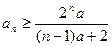 ;
;
 的前n项和
的前n项和 .
.