题目内容
过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若|AB|=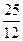 ,|AF|<|BF|,则|AF|为( )
,|AF|<|BF|,则|AF|为( )
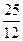 ,|AF|<|BF|,则|AF|为( )
,|AF|<|BF|,则|AF|为( )A.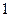 | B.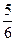 | C.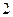 | D.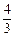 |
B
设过抛物线焦点的直线为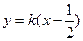 ,联立得
,联立得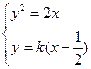 整理得k2x2-(k2+2)x+
整理得k2x2-(k2+2)x+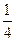 k2=0,
k2=0,
x1+x2=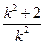 ,x1x2=
,x1x2=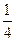 .
.
|AB|=x1+x2+1=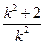 +1=
+1=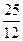 ,得k2=24,
,得k2=24,
代入k2x2-(k2+2)x+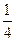 k2=0得12x2-13x+3=0,
k2=0得12x2-13x+3=0,
解得x1=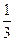 ,x2=
,x2=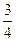 .又|AF|<|BF|,
.又|AF|<|BF|,
故|AF|=x1+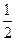 =
=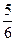 .选B
.选B
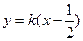 ,联立得
,联立得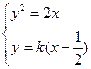 整理得k2x2-(k2+2)x+
整理得k2x2-(k2+2)x+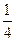 k2=0,
k2=0,x1+x2=
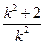 ,x1x2=
,x1x2=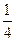 .
.|AB|=x1+x2+1=
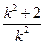 +1=
+1=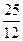 ,得k2=24,
,得k2=24,代入k2x2-(k2+2)x+
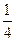 k2=0得12x2-13x+3=0,
k2=0得12x2-13x+3=0,解得x1=
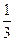 ,x2=
,x2=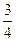 .又|AF|<|BF|,
.又|AF|<|BF|,故|AF|=x1+
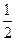 =
=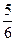 .选B
.选B
练习册系列答案
相关题目
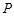 是抛物线
是抛物线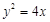 上一点,
上一点, ,则点
,则点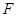 在
在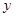 轴正半轴上,过
轴正半轴上,过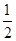 的直线
的直线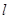 和
和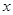 轴交于点
轴交于点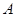 ,且
,且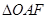 (
(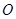 为坐标原点)的面积为
为坐标原点)的面积为 ,求抛物线的标准方程.
,求抛物线的标准方程.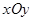 中,已知动点
中,已知动点 到点
到点 的距离为
的距离为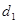 ,到
,到 轴的距离为
轴的距离为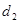 ,且
,且 .
.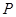 的轨迹
的轨迹 的方程;
的方程;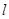 斜率为1且过点
斜率为1且过点 ,其与轨迹
,其与轨迹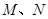 ,求
,求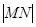 的值.
的值.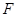 是抛物线
是抛物线 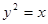 的焦点,
的焦点,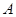 、
、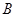 是该抛物线上的两点,
是该抛物线上的两点,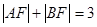 ,则线段
,则线段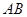 的中点到
的中点到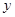 轴的距离为( )
轴的距离为( )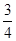
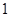
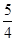
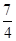
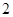 米时,量得水面宽为
米时,量得水面宽为 米.则水面升高
米.则水面升高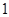 米后,水面
米后,水面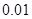 米).
米).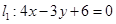 和直线
和直线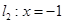 ,抛物线
,抛物线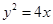 上一动点
上一动点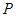 到直线
到直线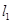
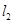 的距离之和的最小值是( )
的距离之和的最小值是( )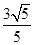
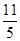
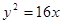 的准线为( )
的准线为( )