题目内容
抛物线的焦点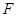 在
在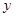 轴正半轴上,过
轴正半轴上,过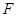 斜率为
斜率为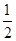 的直线
的直线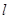 和
和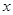 轴交于点
轴交于点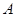 ,且
,且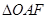 (
(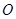 为坐标原点)的面积为
为坐标原点)的面积为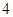 ,求抛物线的标准方程.
,求抛物线的标准方程.
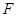 在
在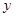 轴正半轴上,过
轴正半轴上,过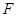 斜率为
斜率为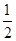 的直线
的直线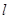 和
和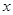 轴交于点
轴交于点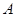 ,且
,且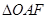 (
(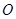 为坐标原点)的面积为
为坐标原点)的面积为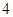 ,求抛物线的标准方程.
,求抛物线的标准方程.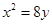 .
.试题分析:先根据抛物线方程表示出F的坐标,进而根据点斜式表示出直线l的方程,求得A的坐标,进而利用三角形面积公式表示出三角形的面积建立等式取得a,则抛物线的方程可得.
解:设抛物线方程为
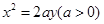
则焦点
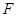 坐标为
坐标为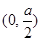 ,直线
,直线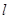 的方程为
的方程为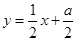 ,
, 它与
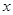 轴的交点为
轴的交点为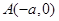 ,
, 所以
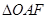 的面积为
的面积为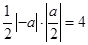 ,
, 解得
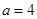 ,所以抛物线方程为
,所以抛物线方程为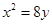 .
.
练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
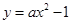 ,直线
,直线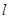 的方程为
的方程为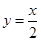 ,点
,点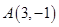 关于直线
关于直线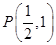 ,求过点
,求过点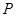 及抛物线与
及抛物线与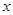 轴两个交点的圆的方程;
轴两个交点的圆的方程;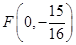 是抛物线的焦点,
是抛物线的焦点,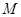 是抛物线上的动点,求
是抛物线上的动点,求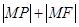 的最小值及此时点
的最小值及此时点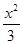 -
-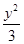 =1相交于A,B两点,若△ABF为等边三角形,则p=________.
=1相交于A,B两点,若△ABF为等边三角形,则p=________.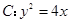 的焦点为
的焦点为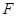 ,
,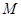 为抛物线
为抛物线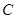 上一点,
上一点,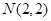 ,则
,则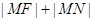 的取值范围是 .
的取值范围是 .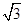
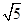
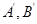 ,则
,则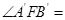 ( )
( )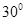 B.
B.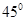 C.
C.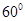 D.
D.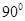
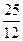 ,|AF|<|BF|,则|AF|为( )
,|AF|<|BF|,则|AF|为( )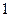
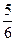
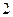
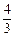
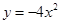 的焦点坐标为.
的焦点坐标为.