题目内容
【题目】设 A(x1 , y1),B(x2 , y2)是函数f(x)=x﹣ ![]() 的图象上任意两点,若 M为 A,B的中点,且 M的横坐标为1.
的图象上任意两点,若 M为 A,B的中点,且 M的横坐标为1.
(1)求y1+y2;
(2)若Tn= ![]() ,n∈N* , 求 Tn;
,n∈N* , 求 Tn;
(3)已知数列{an}的通项公式an= ![]() (n≥1,n∈N*),数列{an}的前n项和为Sn , 若不等式2nSn<m2n﹣4Tn+5对任意n∈N*恒成立,求m的取值范围.
(n≥1,n∈N*),数列{an}的前n项和为Sn , 若不等式2nSn<m2n﹣4Tn+5对任意n∈N*恒成立,求m的取值范围.
【答案】
(1)解:由已知点M为线段AB的中点,则:x1+x2=2,
∴ ![]()
(2)解:由(1),当x1+x2=2时,有f(x1)+f(x2)=2,
故 ![]()
由Tn= ![]() ,
,
Tn= ![]() ,
,
2Tn= ![]() =
= ![]() ×2n×2=2n,
×2n×2=2n,
∴Tn=n
(3)解:由已知:Sn=1+ ![]() ,
,
![]() =
= ![]() +…+
+…+ ![]() ,
, ![]() ,
,
∴Sn=3﹣ ![]() .
.
不等式2nSn<m2n﹣4Tn+5即32n﹣(n+3)<m2n﹣4n+5,
也即(m﹣3)2n>3n﹣8,即m﹣3> ![]() 恒成立,
恒成立,
故只需 ![]() .
.
令bn= ![]() ,
,
当n≥2时,bn﹣bn﹣1= ![]() ,
,
当n≤4时,bn﹣bn﹣1>0,当n≥5时,bn﹣bn﹣1<0,
故b1<b2<b3<b4; b4>b5>b6>
故(bn)max=b4= ![]() ,
,
∴m﹣3> ![]() ,解得:m>
,解得:m> ![]()
【解析】(1)利用中点坐标公式即可得出;(2)由(1),当x1+x2=2时,有f(x1)+f(x2)=2,利用此结论可得Tn . (3)利用“错位相减法”、等比数列的前n项和公式即可得出Sn . 不等式2nSn<m2n﹣4Tn+5,即m﹣3> ![]() 恒成立,故只需
恒成立,故只需 ![]() .令bn=
.令bn= ![]() ,研究其单调性即可得出.
,研究其单调性即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系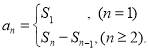 .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目

