题目内容
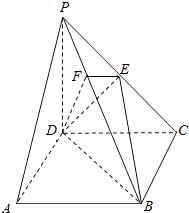
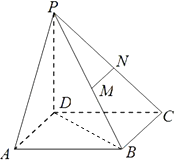
【题目】如图，已知四棱锥P﹣ABCD中，PD⊥底面ABCD，且底面ABCD是边长为2的正方形，M、N分别为PB、PC的中点． 
（1）证明：MN∥平面PAD；
（2）若PB与平面ABCD所成的角为45°，求三棱锥C﹣BDN的体积V．
【答案】
（1）证明：∵M，N是PB，PC的中点，
∴MN∥BC，又BC∥AD，
∴MN∥AD，又MN平面PAD，AD平面PAD，
∴MN∥平面PAD
（2）证明：连接BD，则BD=2 
，
∵PD⊥底面ABCD，
∴∠PBD为PB与平面ABCD所成的角，
∴∠PBD=45°，
∴PD=BD=2 ，
∵N为PC的中点，
∴N到平面ABCD的距离h= 
PD= ，
∴VC﹣BDN=VN﹣BCD= 
= 
= 
．
【解析】（1）由MN∥BC∥AD即可得出MN∥AD，从而得出结论；（2）连接BD，由PD=BD=2 得出N到平面ABCD的距离为h= ，则VC﹣BDN=VN﹣BCD= ．
【考点精析】认真审题，首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)．
期末集结号系列答案
【题目】某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下表所示．
组号 | 分组 | 频数 | 频率 |
第1组 | [160，165） | 5 | 0.050 |
第2组 | [165，170） | n | 0.350 |
第3组 | [170，175） | 30 | p |
第4组 | [175，180） | 20 | 0.200 |
第5组 | [180，185] | 10 | 0.100 |
合计 | 100 | 1.000 |
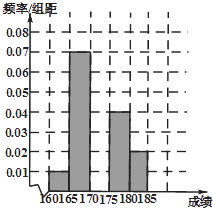
（1）求频率分布表中n，p的值，并补充完整相应的频率分布直方图；
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试，则第3、4、5组每组各抽取多少名学生进入第二轮面试？
（3）在（2）的前提下，学校决定从6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有1名学生被甲考官面试的概率．
【题目】雾霾天气是一种大气污染状态，PM2.5被认为是造成雾霾天气的“元凶”，PM2.5日均值越小，空气质量越好．国家环境标准设定的PM2.5日均值（微克/立方米）与空气质量等级对应关系如表：
PM2.5日均值 | 0﹣﹣35 | 35﹣﹣75 | 75﹣﹣115 | 115﹣﹣150 | 150﹣﹣250 | 250以上 |
空气质量等级 | 1级 | 2级 | 3级 | 4级 | 5级 | 6级 |
由某市城市环境监测网获得4月份某5天甲、乙两城市的空气质量指数数据，用茎叶图表示，如图所示．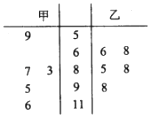
（1）试根据统计数据，分别写出两城区的PM2.5日均值的中位数，并从中位数角度判断哪个城区的空气质量较好？
（2）考虑用频率估计概率的方法，试根据统计数据，估计甲城区某一天空气质量等级为3
（3）分别从甲、乙两个城区的统计数据中任取一个，试求这两城区空气质量等级相同的概率．
