题目内容
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
【答案】
(1)解:由g(x)=2x2﹣4x﹣16<0,得x2﹣2x﹣8<0,
即(x+2)(x﹣4)<0,解得﹣2<x<4.
所以不等式g(x)<0的解集为{x|﹣2<x<4}
(2)解:因为f(x)=x2﹣2x﹣8,
当x>2时,f(x)≥(m+2)x﹣m﹣15成立,
则x2﹣2x﹣8≥(m+2)x﹣m﹣15成立,
即x2﹣4x+7≥m(x﹣1).
所以对一切x>2,均有不等式 ![]() 成立.
成立.
而 ![]() (当x=3时等号成立).
(当x=3时等号成立).
所以实数m的取值范围是(﹣∞,2]
【解析】(1)直接因式分解后求解不等式的解集;(2)把函数f(x)的解析式代入f(x)≥(m+2)x﹣m﹣15,分离变量m后利用基本不等式求解m的取值范围.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
【题目】某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | n | 0.350 |
第3组 | [170,175) | 30 | p |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185] | 10 | 0.100 |
合计 | 100 | 1.000 |
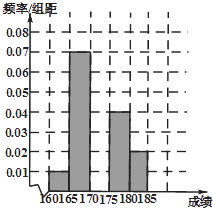
(1)求频率分布表中n,p的值,并补充完整相应的频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.