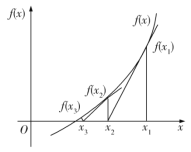
题目内容
【题目】某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,设公司计划一天内安排生产A产品x吨,B产品y吨.
(I)用x,y列出满足条件的数学关系式,并在下面的坐标系中画出相应的平面区域;
(II)该公司每天需生产A,B产品各多少吨可获得最大利润,最大利润是多少?

【答案】(Ⅰ)见解析(Ⅱ)该公司每天需生产甲产品40吨,乙产品10吨可获得最大利润,最大利润为14000元.
【解析】
(Ⅰ)由题意得到变量x,y满足的条件即可得到所求,然后在坐标系内画出图形即可.(Ⅱ)由题意的利润z=300x+200y,然后据线性规划的有关知识解题可得所求.
(I)设该公司一天安排生产甲产品x吨,乙产品y吨,则x,y满足条件的数学关系式为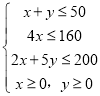 .
.
画出该二元一次不等式组表示的平面区域(可行域)如下图所示.
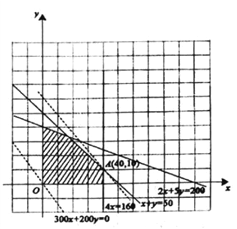
(II)设利润为z元,由题意得z=300x+200y,
可得![]() ,
,
平移直线![]() ,结合图形可得当直线
,结合图形可得当直线![]() 经过可行域上的点A时,截距
经过可行域上的点A时,截距![]() 最大,此时z页最大.
最大,此时z页最大.
解方程组![]() 得
得![]() ,即
,即![]() .
.
∴![]() =300x+200y=14000.
=300x+200y=14000.
答:该公司每天需生产甲产品40吨,乙产品10吨时可获得最大利润,且最大利润为14000元.

【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y万元有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
附注:①参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]()
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
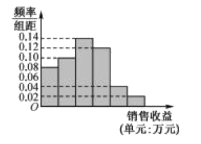
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司在若干地区各投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 3 | 7 |
由表中的数据显示,![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.(参考公式:
的回归直线方程.(参考公式: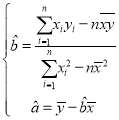 )
)
【题目】某高校在2016年的自主招生考试成绩中随机抽取100位学生的笔试成绩,按成绩分组,得到的频率分布表如下所示.
(1)请先求出频率分布表中①②位置相应的数据,再在答题纸上完成下列频率分布直方图(如图所示);
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| ① | 0.350 |
第3组 |
| 30 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
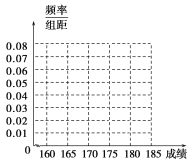
频率分布直方图
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6位学生进入第二轮面试,求第3、4、5组每组各抽取多少位学生进入第二轮面试;
(3)在(2)的前提下,学校决定在6位学生中随机抽取2位学生接受A考官进行面试,求第4组至少有一位学生被考官A面试的概率.