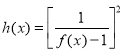Question

【题目】某高校在2016年的自主招生考试成绩中随机抽取100位学生的笔试成绩，按成绩分组，得到的频率分布表如下所示．

（1）请先求出频率分布表中①②位置相应的数据，再在答题纸上完成下列频率分布直方图（如图所示）；

组号	分组	频数	频率
第1组		5	0.050
第2组		①	0.350
第3组		30	②
第4组		20	0.200
第5组		10	0.100
合计		100	1.000

频率分布直方图

（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6位学生进入第二轮面试，求第3、4、5组每组各抽取多少位学生进入第二轮面试；

（3）在（2）的前提下，学校决定在6位学生中随机抽取2位学生接受A考官进行面试，求第4组至少有一位学生被考官A面试的概率．

Answer 1

【答案】（1）人；；（2）3人、2人、1人；（3）

【解析】

（1）利用总数和第组的频率可算出第组的频数，利用第组的频数和总数可算出第组的频率，再根据频率分布表的数据画出频率直方图即可.

（2）首先求出抽样比，再利用分层抽样即可得到第3、4、5组分别抽取的人数.

（3）首先求出从名同学抽取名学生的全部基本事件，再求出至少有一位学生是第组的基本事件个数，利用古典概型公式计算即可得到答案.

（1）由题可知，第2组的频数为（人），

第3组的频率为，频率分布直方图如图所示．

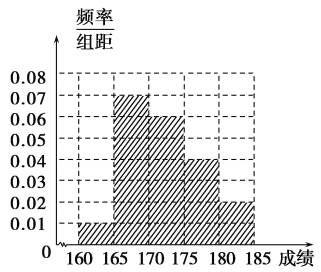
（2）因为第3、4、5组共有60名学生，抽样比.

第3组抽取：（人），第4组：（人），

第5组：（人），所以第3、4、5组分别抽取3人、2人、1人．

（3）设第3组的3位同学为，第4组的2位同学为，

第5组的1位同学为，则从六位同学中抽两位同学有15种可能，如下：

，，，，，，，，，，，，，，．

第4组至少有一位同学入选的有：

，，，，，，

，，，共9种可能．

所以第4组的2位同学至少有一位同学入选的概率为．