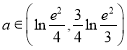题目内容
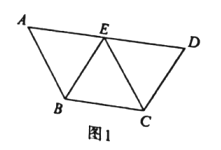
【题目】如图1,在等腰梯形ABCD中,![]() ,
,![]() ,
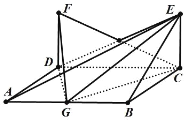
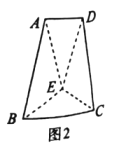
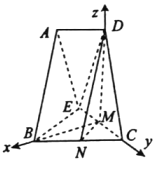
,![]() ,E为AD的中点.现分别沿BE,EC将△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,连接AD,如图2.
,E为AD的中点.现分别沿BE,EC将△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,连接AD,如图2.
(1)若在平面BCE内存在点G,使得GD∥平面ABE,请问点G的轨迹是什么图形?并说明理由.
(2)求平面AED与平面BCE所成锐二面角的余弦值.
【答案】(1)点G的轨迹是直线MN,见解析;(2)![]()
【解析】
(1)分别取![]() 和
和![]() 的中点
的中点![]() 和
和![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,根据线线平行可证明平面
,根据线线平行可证明平面![]() 平面
平面![]() ,则可判断点
,则可判断点![]() 的轨迹;(2)以点
的轨迹;(2)以点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,分别求两个平面的法向量
轴,建立空间直角坐标系,分别求两个平面的法向量![]() ,代入公式
,代入公式![]() 求解.
求解.
(1)点G的轨迹是直线MN.
理由:如图,分别取BC和CE的中点N和M,连接DM,MN,ND,则MN//BE.
又MN![]() 平面BEA,BE
平面BEA,BE![]() 平面BEA,所以MN//平面BEA.
平面BEA,所以MN//平面BEA.
依题意有△ABE,△BCE,△ECD均为边长为2的正三角形,所以MD⊥CE.
又平面ECD⊥平面BCE,则MD⊥平面BCE.又平面ABE⊥平面BCE,所以MD//平面BEA.
所以平面NMD//平面BEA,则点G的轨迹是直线MN.
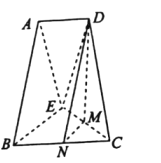
(2)如图,以点M为坐标原点,MB所在直线为x轴,MC所在直线为y轴,MD所在直线为z轴,建立空间直角坐标系,则E(0,-1,0),D(0,0,![]() ),A
),A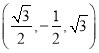 ,所以
,所以 ,
,![]() .
.
设平面AED的法向量为![]() ,则
,则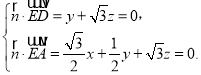
取![]() ,得
,得![]() . 取平面BCE的一个法向量为
. 取平面BCE的一个法向量为![]() ,
,
则![]() , 所以平面AED与平面BCE所成锐二面角的余弦值为
, 所以平面AED与平面BCE所成锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目