题目内容
【题目】已知函数f(x)=ex+e-x,其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求实数m的取值范围;
(3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(-![]() +3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
+3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
【答案】(1)见解析(2)m的取值范围是[-∞,-![]() .](3)见解析
.](3)见解析
【解析】
(1)根据函数奇偶性的定义即可证明f(x)是R上的偶函数;
(2)利用参数分离法,将不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立转化为求最值问题,即可求实数m的取值范围;
(3)构造函数,利用函数的单调性,最值与单调性之间的关系,分类讨论即可得解.
解析: (1) 因为对任意x∈R,
都有f(-x)=e-x+e-(-x)=e-x+ex=f(x),
所以f(x)是R上的偶函数.
(2) 由条件知m(ex+e-x-1)≤e-x-1在(0,+∞)上恒成立.
令t=ex(x>0),则t>1,所以m≤-![]() =-
=-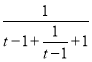 对任意t>1成立.
对任意t>1成立.
因为![]() ,所以-
,所以-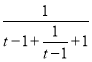 ≥-
≥-![]() ,
,
当且仅当t=2,即x=ln2时等号成立.
因此实数m的取值范围是(-∞,-![]() ).
).
(3) 令函数g(x)=ex+![]() -a(-x3+3x),则g′(x)=ex-
-a(-x3+3x),则g′(x)=ex-![]() +3a(x2-1).
+3a(x2-1).
当x≥1时,ex-![]() >0,x2-1≥0.
>0,x2-1≥0.
又a>0,故g′(x)>0,所以g(x)是[1,+∞)上的单调增函数,
因此g(x)在[1,+∞)上的最小值是g(1)=e+e-1-2a.
由于存在x0∈[1,+∞),使ex0+e-x0-a(-![]() +3x0)<0成立,
+3x0)<0成立,
当且仅当最小值g(1)<0.
故e+e-1-2a<0,即a>![]() .
.
解法1:令函数h(x)=x-(e-1)lnx-1,则h′(x)=1-![]() .
.
令h′(x)=0,得x=e-1.
当x∈(0,e-1)时,h′(x)<0,故h(x)在(0,e-1)上是单调减函数;当x∈(e-1,+∞)时,h′(x)>0,故h(x)在(e-1,+∞)上是单调增函数.
所以h(x)在(0,+∞)上的最小值是h(e-1).
注意到h(1)=h(e)=0,在区间(0,1)和(e,+∞)上,h(x)>0;在区间(1,e)上,h(x)<0.
①当a∈![]() ,e(1,e)时,h(a)<0,即a-1<(e-1)lna,从而ea-1<ae-1;
,e(1,e)时,h(a)<0,即a-1<(e-1)lna,从而ea-1<ae-1;
②当a=e时,ea-1=ae-1;
③当a∈(e,+∞)(e-1,+∞)时,h(a)>h(e)=0,即a-1>(e-1)lna,故ea-1>ae-1.
综上所述,当a∈![]() ,e时,ea-1<ae-1;
,e时,ea-1<ae-1;
当a=e时,ea-1=ae-1;
当a∈(e,+∞)时,ea-1>ae-1.
解法2:由于ea-1与ae-1均为正数,同取自然底数的对数,
即比较(a-1)lne与(e-1)lna的大小,即比较![]() 与
与![]() 的大小.
的大小.
构造函数h(x)=![]() ,则h′(x)=
,则h′(x)=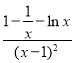
设m(x)=1-![]() -lnx,则m′(x)=
-lnx,则m′(x)=![]() .
.
令m′(x)=0,得x=1.当x>1时,m′(x)<0;当0<x<1时,m′(x)>0.所以m(x)在(1,+∞)上单调递减,此时m(x)<m(1)=0,
所以h′(x)<0在(1,+∞)上恒成立,所以h(x)=![]() 在(1,+∞)上单调递减.
在(1,+∞)上单调递减.
所以当![]() <a<e时,ae-1>ea-1;当a=e时,ea-1=ae-1;当a>e时,ae-1<ea-1.
<a<e时,ae-1>ea-1;当a=e时,ea-1=ae-1;当a>e时,ae-1<ea-1.
解法3 因为ae-1=e(e-1)lna,所以![]() =e(e-1)lna-(a-1),故只要比较a-1与(e-1)lna的大小.
=e(e-1)lna-(a-1),故只要比较a-1与(e-1)lna的大小.
令h(x)=(e-1)lnx-(x-1),那么h′(x)=![]() -1.
-1.
令h′(x)=0,得x=e-1.
当x>e-1时,h′(x)<0;当0<x<e-1时,h′(x)>0.
所以h(x)在(0,e-1)上是增函数;在(e-1,+∞)上是减函数.
又h(e)=0,h(1)=0,则h(e-1)>0,h(![]() )>0.那么当
)>0.那么当![]() <a<e时,h(a)>0,所以eh(a)>1,所以ae-1>ea-1;当a=e时,h(a)=0,所以ea-1=ae-1;当a>e时,h(a)<0,所以0<eh(a)<1,所以ae-1<ea-1.
<a<e时,h(a)>0,所以eh(a)>1,所以ae-1>ea-1;当a=e时,h(a)=0,所以ea-1=ae-1;当a>e时,h(a)<0,所以0<eh(a)<1,所以ae-1<ea-1.
综上所述,当![]() <a<e时,ae-1>ea-1;当a=e时,ea-1=ae-1;当a>e时,ae-1<ea-1.
<a<e时,ae-1>ea-1;当a=e时,ea-1=ae-1;当a>e时,ae-1<ea-1.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:
个税税额=应纳税所得额×税率-速算扣除数.
应纳税所得额的计算公式为:
应纳税所得额=综合所得收入额-免征额-专项扣除-专项附加扣除-依法确定的其他扣除.
其中免征额为每年60000元,税率与速算扣除数见下表:
级数 | 全年应纳税所得额所在区间 | 税率( | 速算扣除数 |
1 |
| 3 | 0 |
2 |
| 10 | 2520 |
3 |
| 20 | 16920 |
4 |
| 25 | 31920 |
5 |
| 30 | 52920 |
6 |
| 35 | 85920 |
7 |
| 45 | 181920 |
备注:
“专项扣除”包括基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金。
“专项附加扣除”包括子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等支出。
“其他扣除”是指除上述免征额、专项扣除、专项附加扣除之外,由国务院决定以扣除方式减少纳税的优惠政策规定的费用。
某人全年综合所得收入额为160000元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是![]() ,
,![]() ,
,![]() ,
,![]() ,专项附加扣除是24000元,依法确定其他扣除是0元,那么他全年应缴纳综合所得个税____元.
,专项附加扣除是24000元,依法确定其他扣除是0元,那么他全年应缴纳综合所得个税____元.
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.

(1)用样本估计总体,以频率作为概率,若在![]() 两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: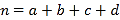 ,其中
,其中![]() )
)