题目内容
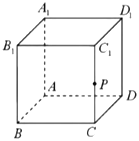
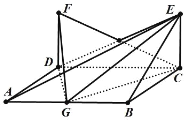
【题目】如图，在四棱锥 E ABCD 中， EC 底面 ABCD ， FD / /EC ，底面 ABCD 为矩形， G 为线段 AB 的中点， CG DG，CD DF CE 2 ，则四棱锥 E ABCD与三棱锥 F CDG 的公共部分的体积为________________ .
【答案】
.
【解析】
根据题意，公共部分的体积应该为两个三棱锥体积之差，据此求解.
连接EF，在四边形EFDC中，
因为FD//EC，确定一个平面，
则DE与FC必然相交，记其交点为M；
同理，因为EF//AB，确定一个平面，
则FG与EA必然相交，记其交点为N，连接MN，如图所示：
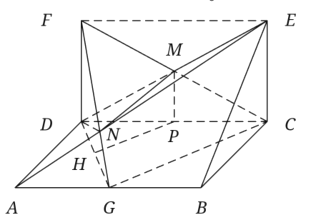
则公共部分的体积
因为
，故
平面FDG，
则
在三角形EFN和三角形ANG中，因为EF//AG，且
故可得N为FG的三等分点，
则
又因为M点为FC的中点，
故M点到平面FDN的距离为C点到平面FDN距离的
故
故公共部分的体积为：
.
故答案为：
.
备战中考寒假系列答案
【题目】依法纳税是每个公民应尽的义务，个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税（简称个税）．2019年1月1日起，个税税额根据应纳税所得额、税率和速算扣除数确定，计算公式为：
个税税额＝应纳税所得额×税率－速算扣除数．
应纳税所得额的计算公式为：
应纳税所得额＝综合所得收入额－免征额－专项扣除－专项附加扣除－依法确定的其他扣除．
其中免征额为每年60000元，税率与速算扣除数见下表：
级数 | 全年应纳税所得额所在区间 | 税率（ | 速算扣除数 |
1 |
| 3 | 0 |
2 |
| 10 | 2520 |
3 |
| 20 | 16920 |
4 |
| 25 | 31920 |
5 |
| 30 | 52920 |
6 |
| 35 | 85920 |
7 |
| 45 | 181920 |
备注：
“专项扣除”包括基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金。
“专项附加扣除”包括子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等支出。
“其他扣除”是指除上述免征额、专项扣除、专项附加扣除之外，由国务院决定以扣除方式减少纳税的优惠政策规定的费用。
某人全年综合所得收入额为160000元，假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是
，
，
，
，专项附加扣除是24000元，依法确定其他扣除是0元，那么他全年应缴纳综合所得个税____元．
