题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() .
.
(1)讨论![]() 的单调区间
的单调区间
(2)当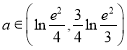 时,存在
时,存在![]() ,使得对任意
,使得对任意![]() 均有
均有![]() ,求实数M的最大值.
,求实数M的最大值.
【答案】(1)见解析;(2)1
【解析】
(1)先求导,再分类讨论,根据导数和函数单调性的关系即可求出单调区间,
(2)根据(1)的结论可得故存在![]() ,使得
,使得![]() ,且当
,且当![]() 时
时![]() 恒成立,由
恒成立,由![]() 可得
可得![]() ,再构造函数
,再构造函数![]() (
(![]() ),利用导数求出函数的最值即可.
),利用导数求出函数的最值即可.
(1)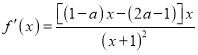 ,
,
①![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
②![]() 时,令
时,令![]() 得
得![]() ,故增区间为
,故增区间为![]() ,
,
令![]() 得
得![]() ,故减区间为
,故减区间为![]() ;
;
③![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减.
上单调递减.
(2)易知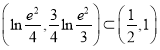 ,
,
由(1)知:![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
则![]() ,
,
又![]() ,
,
故存在![]() ,使得
,使得![]() ,
,
且当![]() 时
时![]() 恒成立,
恒成立,
故![]() .
.
由![]() 可得
可得![]() ,
,
设![]() (
(![]() ),
),
则![]() ,
,
令![]() (
(![]() ),
),
则![]() ,
,
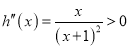 ,
,
则![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,
,
则![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,
,
则![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
![]() ,
,![]() ,故
,故![]() ,
,
则![]() ,
,
又![]() ,故
,故![]() ,即M的最大值为1.
,即M的最大值为1.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.

(1)用样本估计总体,以频率作为概率,若在![]() 两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: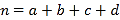 ,其中
,其中![]() )
)