题目内容
2.已知数列{an}、{bn}中,对任何正整数n都有:a1bn+a2bn-1+a3bn-2…+an-1b2+anb1=2n+1-n-2.(1)若数列{an}是首项和公差都是1的等差数列,求b1,b2,并证明数列{bn}是等比数列;
(2)若数列{bn}是等比数列,数列{an}是否是等差数列,若是请求出通项公式,若不是请说明理由;
(3)若数列{an}是等差数列,数列{bn}是等比数列,求证:$\frac{1}{{a}_{1}{b}_{1}}$+$\frac{1}{{a}_{2}{b}_{2}}$+…+$\frac{1}{{a}_{n}{b}_{n}}$<$\frac{3}{2}$.
分析 (1)利用递推关系式得出bn+2bn-1+3bn-2+…+(n-1)b2+nb1=2n+1-n-2,bn-1+2bn-2+3bn-3+…+(n-2)b2+(n-1)b1=2n-n-1,(n≥2),
相减得出bn+bn-1+…+b2+b1=2n-1,利用前n项的和Sn求解bn=2n-1,证明即可.
(2)bqn-1a1+bqn-2a2+bqn-3a3+…+bqan-1+ban=2n+1-n-2,又bqn-2a1+bqn-3a2+bqn-4a3+…+ban-1=2n-n-1(n≥2),
an=$\frac{2-q}{b}$×2n$+\frac{q-1}{b}$×n$+\frac{q-2}{b}$,讨论求解即可.
(3)求解$\frac{1}{{a}_{1}{b}_{1}}$+$\frac{1}{{a}_{2}{b}_{2}}$+…+$\frac{1}{{a}_{n}{b}_{n}}$=$\frac{1}{1×1}$$+\frac{1}{2×2}$$+\frac{1}{3×{2}^{2}}$$+\frac{1}{4×{2}^{3}}$+…+$\frac{1}{n×{2}^{n-1}}$<$\frac{1}{1×1}$$+\frac{1}{2×2}$$+\frac{1}{2×{2}^{2}}$+$\frac{1}{2×{2}^{3}}$+…+$\frac{1}{2×{2}^{n-1}}$求解为和的形式,放缩即可.
解答 解:(1)b1=1,b2=2,
依题意数列{an}的通项公式是an=n,
故等式即为bn+2bn-1+3bn-2+…+(n-1)b2+nb1=2n+1-n-2,
bn-1+2bn-2+3bn-3+…+(n-2)b2+(n-1)b1=2n-n-1,(n≥2),
两式相减可得bn+bn-1+…+b2+b1=2n-1,
得bn=2n-1,数列{bn}是首项为1,公比为2的等比数列.
(2)设等比数列{bn}的首项为b,公比为q,则bn=bqn-1,
从而有:bqn-1a1+bqn-2a2+bqn-3a3+…+bqan-1+ban=2n+1-n-2,
又bqn-2a1+bqn-3a2+bqn-4a3+…+ban-1=2n-n-1(n≥2),
故(2n-n-1)q+ban=2n+1-n-2,
an=$\frac{2-q}{b}$×2n$+\frac{q-1}{b}$×n$+\frac{q-2}{b}$,
要使an+1-an是与n无关的常数,必需q=2,
即①当等比数列{bn}的公比q=2时,数列{an}是等差数列,其通项公式是an=$\frac{n}{b}$;
②当等比数列{bn}的公比不是2时,数列{an}不是等差数列.
(3)由(2)知anbn=n•2n-1,
显然n=1,2时$\frac{1}{{a}_{1}{b}_{1}}$+$\frac{1}{{a}_{2}{b}_{2}}$+…+$\frac{1}{{a}_{n}{b}_{n}}$<$\frac{3}{2}$,
当n≥3时$\frac{1}{{a}_{1}{b}_{1}}$+$\frac{1}{{a}_{2}{b}_{2}}$+…+$\frac{1}{{a}_{n}{b}_{n}}$=$\frac{1}{1×1}$$+\frac{1}{2×2}$$+\frac{1}{3×{2}^{2}}$$+\frac{1}{4×{2}^{3}}$+…+$\frac{1}{n×{2}^{n-1}}$<$\frac{1}{1×1}$$+\frac{1}{2×2}$$+\frac{1}{2×{2}^{2}}$+$\frac{1}{2×{2}^{3}}$+…+$\frac{1}{2×{2}^{n-1}}$=
1$+\frac{1}{2×2}$$•\frac{1-(\frac{1}{2})^{n-1}}{1-\frac{1}{2}}$=$\frac{3}{2}$$-\frac{1}{{2}^{n}}$$<\frac{3}{2}$.
点评 本题考查了数列的综合应用,递推关系式的运用,不等式,放缩法求解证明不等式,属于综合题目,难度较大,化简较麻烦.

 阅读快车系列答案
阅读快车系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
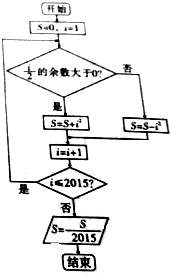
| A. | 1006 | B. | 1008 | C. | 2015 | D. | 2016 |