题目内容
已知向量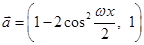 ,
,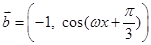 ,
,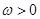 ,点A、B为函数
,点A、B为函数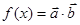 的相邻两个零点,AB=π.
的相邻两个零点,AB=π.
(1)求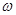 的值;
的值;
(2)若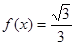 ,
,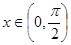 ,求
,求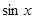 的值;
的值;
(3)求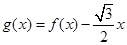 在区间
在区间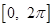 上的单调递减区间.
上的单调递减区间.
(1)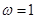 ;(2)
;(2)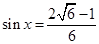 ;(3)
;(3)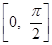 ,
,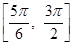 .
.
解析试题分析: (1)由向量的数量积可得: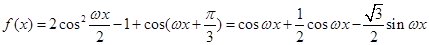
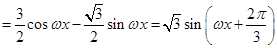 .
.
这个函数相邻两个零点间的距离等于半个周期,再利用求周期的公式可得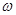 的值.
的值.
(2)由(1)得 ,则
,则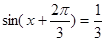 .
.
这里不能展开来求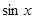 ,而应考虑凑角:
,而应考虑凑角: 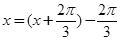 ,这样再利用差角的正弦公式就可以求出
,这样再利用差角的正弦公式就可以求出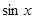 的值;
的值;
(3)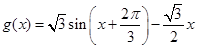 ,这是一个三角函数与一个一次函数的差构成的函数,故可通过导数来求它的单调区间.
,这是一个三角函数与一个一次函数的差构成的函数,故可通过导数来求它的单调区间.
试题解析:(1)
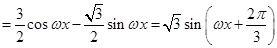 , 3分
, 3分
由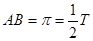 ,得
,得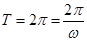 ,则
,则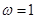 . 4分
. 4分
(2)由(1)得 ,则
,则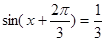 .
.
由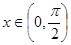 ,得
,得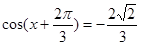 , 6分
, 6分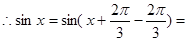
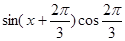
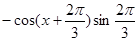
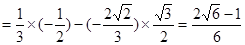 . 8分
. 8分
(3)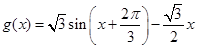 ,
,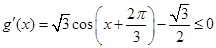 ,
,
∴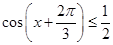 , 10分
, 10分
∴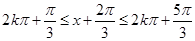 (
(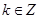 ),
),
即 (
(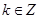 ),
),
又 ,
,
∴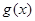 在区间
在区间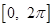 上的单调递减区间为
上的单调递减区间为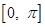 ,
,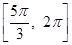 12分
12分
考点:1、向量的数量积;2、三角函数的周期;3、三角变换;4、导数的应用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
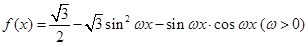 ,且
,且 图象的相邻两条对称轴间的距离为
图象的相邻两条对称轴间的距离为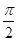 ,
,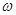 的值;
的值;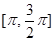 上的值域.
上的值域.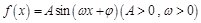 的一段图象如图所示.
的一段图象如图所示.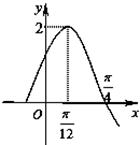
 的解析式;
的解析式; 求函数
求函数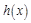 的单调递增区间.
的单调递增区间.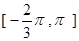 上的函数
上的函数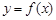 的图象关于直线
的图象关于直线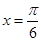 对称,当
对称,当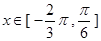 时函数
时函数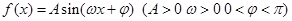 图象如图所示.
图象如图所示. 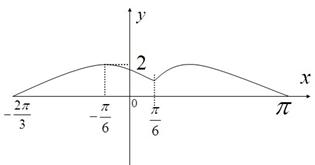
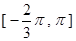 的表达式;
的表达式;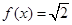 的解;
的解; 的值,使得
的值,使得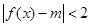 在
在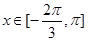 上恒成立;若存在,求出
上恒成立;若存在,求出 (其中
(其中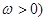 的最小正周期为
的最小正周期为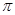 .
.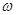 的值,并求函数
的值,并求函数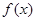 的单调递减区间;
的单调递减区间;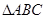 中,
中, 分别是角
分别是角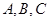 的对边,若
的对边,若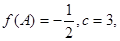
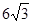 ,求
,求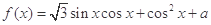 .
.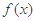 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;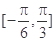 上的最大值与最小值的和为
上的最大值与最小值的和为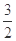 ,求
,求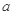 的值.
的值. 中,已知内角
中,已知内角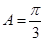 ,边
,边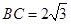 .设内角
.设内角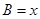 ,
, .
.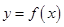 的解析式和定义域;
的解析式和定义域;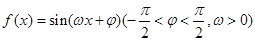 的最小正周期为
的最小正周期为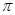 ,其图像经过点
,其图像经过点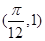
 的解析式;
的解析式;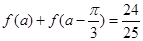 且
且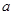 为锐角,求
为锐角,求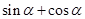 的值.
的值.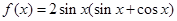 .
.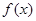 的最小正周期;
的最小正周期;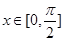 时,求
时,求