题目内容
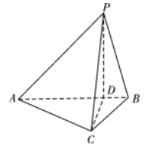
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,
,![]() 平面
平面![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先由线面垂直的判定定理,证明![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 平面
平面![]() ;
;
(2)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 与平面
与平面![]() 的一个法向量,根据向量夹角公式,求出两向量夹角的余弦值,进而可得出结果.
的一个法向量,根据向量夹角公式,求出两向量夹角的余弦值,进而可得出结果.
(1)因为![]() ,
,![]() ,
,
所以![]()
所以![]() 是直角三角形,
是直角三角形,![]() ;
;
在![]() 中,由
中,由![]() ,
,![]() ,
,
不妨设![]() ,由
,由![]() 得,
得,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得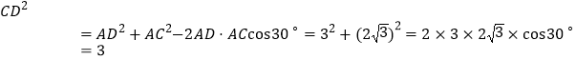 ,
,
故![]() ,
,
所以![]() ,所以
,所以![]() ;
;
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ;
;
(2)因为![]() 平面
平面![]() ,所以
,所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,即
,即![]() ,
,
可得![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,

由(1)得![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() 为平面
为平面![]() 的一个法向量。
的一个法向量。
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
因为![]() ,
,![]() ,
,
则由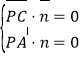 得
得![]()
令![]() ,则
,则![]() ,
,![]() ,
,
则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
故![]()
故二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

【题目】已知某商品每件的生产成本![]() (元)与销售价格
(元)与销售价格![]() (元)具有线性相关关系,对应数据如表所示:
(元)具有线性相关关系,对应数据如表所示:
| 5 | 6 | 7 | 8 |
| 15 | 17 | 21 | 27 |
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该商品的月销售量![]() (千件)与生产成本
(千件)与生产成本![]() (元)的关系为
(元)的关系为![]() ,
,![]() ,根据(1)中求出的线性回归方程,预测当
,根据(1)中求出的线性回归方程,预测当![]() 为何值时,该商品的月销售额最大.
为何值时,该商品的月销售额最大.
附: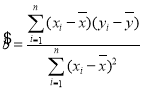 ,
,![]() .
.
【题目】根据新高考改革方案,某地高考由文理分科考试变为“3+3”模式考试.某学校为了解高一年425名学生选课情况,在高一年下学期进行模拟选课,统计得到选课组合排名前4种如下表所示,其中物理、化学、生物为理科,政治、历史、地理为文科,“√”表示选择该科,“×”表示未选择该科,根据统计数据,下列判断错误的是
学科 人数 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 |
124 | √ | √ | × | × | × | √ |
101 | × | × | √ | × | √ | √ |
86 | × | √ | √ | × | × | √ |
74 | √ | × | √ | × | √ | × |
A. 前4种组合中,选择生物学科的学生更倾向选择两理一文组合
B. 前4种组合中,选择两理一文的人数多于选择两文一理的人数
C. 整个高一年段,选择地理学科的人数多于选择其他任一学科的人数
D. 整个高一年段,选择物理学科的人数多于选择生物学科的人数