题目内容
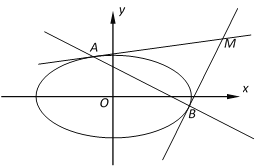
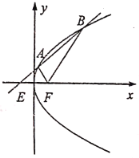
【题目】如图，已知F是抛物线C：
的焦点，过E(﹣l，0)的直线
与抛物线分別交于A，B两点（点A，B在x轴的上方）．
（1）设直线AF，BF的斜率分別为
，
，证明：
；
（2）若
ABF的面积为4，求直线的方程．
【答案】(1)见解析；(2)
.
【解析】
（1）设直线
的方程为x＝my﹣1，A（x1，y1），B（x2，y2），联立抛物线方程利用韦达定理可得
.
（2）S△ABF＝S△EFB﹣S△EFA＝|y1﹣y2|＝
．解得m即可．
（1）当直线的斜率为0时，直线与抛物线只有一个交点，不合题意．
当直线的斜率不为0时，设直线的方程为x＝my﹣1，A（x1，y1），B（x2，y2），
联立抛物线方程可得得y2﹣4my+4＝0，可得y1+y2＝4m，y1y2＝4
∴
.
（2）S△ABF＝S△EFB﹣S△EFA＝|y1﹣y2|＝．
解得m＝
（负值舍去）．
∴直线的方程为：．
练习册系列答案
相关题目
