��Ŀ����
����Ŀ��Ϊ�˹��������Լ�õ磬ʵ�С�����ʽ����ۣ�ij��Զɽ��ÿ���������õ�������Ϊ���������õ���������150�ȣ���0.6Ԫ/���շѣ�����150�ȵ�������250�ȵIJ���ÿ�ȼӼ�0.1Ԫ������250�ȵIJ���ÿ���ټӼ�0.3Ԫ�շ�.
��1����ñ�Զɽ��ij���������õ����![]() ����λ��Ԫ���������õ���
����λ��Ԫ���������õ���![]() ����λ���ȣ��ĺ�������ʽ��
����λ���ȣ��ĺ�������ʽ��
��2����֪�ñ�Զɽ��ƶ���������õ���![]() ����λ���ȣ���û����ھ�ס���˿���
����λ���ȣ���û����ھ�ס���˿���![]() ����λ���ˣ�����Ƶ�����������ع�ϵ��
����λ���ˣ�����Ƶ�����������ع�ϵ��![]() ��
��![]() ��ֵ��ȷ���������������������
��ֵ��ȷ���������������������
| 14 | 15 | 17 | 18 |
| 161 | 168 | 191 | 200 |
������Ϊ����ƶ����ͥ�ľ��ø������ƻ��Ըñ�Զɽ����ƶ����ͥ����һ���ľ��ò������������ֲ���������ѡ��һ�Ǹ��ݸü�ͥ������ÿ��ÿ���²���6Ԫ�����Ǹ����õ���ÿ��ÿ�²���![]() ��
��![]() Ϊ�õ�����Ԫ������ݼ�ͥ����
Ϊ�õ�����Ԫ������ݼ�ͥ����![]() ������һ��ƶ����ͥѡ�����ֲ�����ʽ���Ի�ø���IJ�����
������һ��ƶ����ͥѡ�����ֲ�����ʽ���Ի�ø���IJ�����
�����ع�ֱ��![]() ��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
 ��
��![]() .
.
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
���𰸡���1��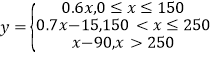 ����2��������
����2��������
����������������1���ɵ�۷������������������÷ֶκ����������ʽ��������2����������С���˷�����ع鷽��![]() ����һ�ַ���
����һ�ַ���![]() ��ÿ�²���
��ÿ�²���![]() Ԫ���ڶ��ַ���
Ԫ���ڶ��ַ���![]() ��ÿ�²���Ϊ
��ÿ�²���Ϊ
![]() ����
����![]() ����
����![]() �����
�����![]() ���Ӷ��ɵý��.
���Ӷ��ɵý��.
�������1����![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ����
����![]() �Ľ���ʽΪ
�Ľ���ʽΪ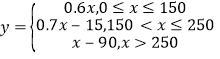 .
.
��2����![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���Իع�ֱ�߷���Ϊ![]() .
.
��һ�ַ���![]() ��ÿ�²���
��ÿ�²���![]() Ԫ���ڶ��ַ���
Ԫ���ڶ��ַ���![]() ��ÿ�²���Ϊ
��ÿ�²���Ϊ
![]() ����
����![]() ��
��
��![]() �����
�����![]() ��
��
�൱����������5��ʱ��ѡ��ڶ��ֲ�����ʽ�ɻ�ø��ಹ��������������5��ʱ��ѡ���һ�ֲ�����ʽ�ɻ�ø��ಹ��.

����Ŀ����֪����![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() �����ֶ�Ӧֵ���±�����֪
�����ֶ�Ӧֵ���±�����֪![]() �ĵ�����
�ĵ�����![]() ��ͼ������ͼ��ʾ��
��ͼ������ͼ��ʾ��
| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
�����й���![]() �����⣺
�����⣺
��![]() ����
Ϊ����![]() ��һ������ֵ�㣻
��һ������ֵ�㣻
�ں���![]() �ļ�Сֵ��Ϊ2��
�ļ�Сֵ��Ϊ2��
�ۺ���![]() ��
��![]() ���Ǽ�������
���Ǽ�������
�������![]() ʱ��
ʱ��![]() �����ֵ��2����ô
�����ֵ��2����ô![]() �����ֵΪ4��
�����ֵΪ4��
�ݵ�![]() ʱ������
ʱ������![]() ��4�����.
��4�����.
������ȷ����������__________��

����Ŀ��������ij��Ϊ�ֻ�ר�����������л�Ϊ�ֻ��Ͽɶȵĵ��飬���ѹ���Ϊ�ֻ���![]() �������У������ȡ
�������У������ȡ![]() ���������䣨��λ���꣩����ͳ�Ƶ�Ƶ���ֲ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
���������䣨��λ���꣩����ͳ�Ƶ�Ƶ���ֲ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��

���飨�꣩ | Ƶ�� |
|
|
|
|
|
|
|
|
|
|
�ϼ� |
|
��1����Ƶ���ֲ�����![]() ��
��![]() ��ֵ������ȫƵ�ʷֲ�ֱ��ͼ��
��ֵ������ȫƵ�ʷֲ�ֱ��ͼ��
��2���ڳ�ȡ����![]() �������У���������
����������������![]() ��
��![]() �ڵ��������÷ֲ�����ķ�����ȡ
�ڵ��������÷ֲ�����ķ�����ȡ![]() �˲μӻ�Ϊ�ֻ���������ִ���
�˲μӻ�Ϊ�ֻ���������ִ���![]() �������ѡȡ
�������ѡȡ![]() �˸�����һ����Ϊ�ֻ�������
�˸�����һ����Ϊ�ֻ�������![]() ����ǡ��
����ǡ��![]() �˵�������
�˵�������![]() �ڵĸ���.
�ڵĸ���.
����Ŀ��ij����ͨ�����������5��ʳƷ����λ�����![]() (����)���������ԭ��������
(����)���������ԭ��������![]() (��)���õ�����ͳ�Ʊ���
(��)���õ�����ͳ�Ʊ���
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | |
����� | 13 | 9 | 8 | 10 | 12 |
ԭ���� | 32 | 23 | 18 | 24 | 28 |
��1����������5�����ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() .
.
��2����֪����ԭ���ϵķ���![]() (Ԫ)������
(Ԫ)������![]() (��)�Ĺ�ϵΪ
(��)�Ĺ�ϵΪ![]() ��
��
Ͷ��ʹ�õ�ÿ��ԭ������Ӧ����������Ϊ700Ԫ�������ԭ����ֻ������������Ϥ���ν��״���Լ��15���˲μӣ�����(1)����������Իع鷽�̣�Ԥ�����Ӧ������ٴ�ԭ���ϣ����ܻ�����������������Ƕ��٣�(ע������![]() ��������
��������![]() ԭ���Ϸ���).
ԭ���Ϸ���).
�ο���ʽ��  ��
�� ![]() .
.
�ο����ݣ� ![]() ��
�� ![]() ��
�� ![]() .
.