题目内容
8.袋中有红、白色球各一个,每次任取一个,有放回地抽三次,(1)写出所有的基本事件;
(2)求三次颜色全相同的概率;
(3)求三次抽取的球中红色球出现的次数多于白色球出现的次数的概率.
分析 (1)写出所有基本事件,求出总个数,
(2)求出三次颜色全相同的基本事件个数,代入古典概型概率公式计算;
(3)求出三次抽取的红球数多于白球数的基本事件个数,代入古典概型概率公式计算
解答 解:(1)由题意,基本事件共有23=8个结果,分别是(红,红,红),(红,红,白),(红,白,红),(白,红,红),
(红,白,白),(白,红,白),(白,白,红),(白,白,白).
(2)三次颜色全相同有2个结果,
∴三次颜色全相同的概率为$\frac{2}{8}$=$\frac{1}{4}$;
(3)三次抽取的红球数多于白球数的有4个结果,
∴三次抽取的红球数多于白球数的概率为$\frac{4}{8}$=$\frac{1}{2}$.
点评 本题考查了等可能事件的概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
3.已知$\overrightarrow{OA}$=$\overrightarrow{i}+3\overrightarrow{k}$,$\overrightarrow{OB}$=$\overrightarrow{j}+3\overrightarrow{k}$,则△OAB的面积为( )
| A. | $\frac{\sqrt{19}}{2}$ | B. | 2$\sqrt{19}$ | C. | $\sqrt{19}$ | D. | 8$\sqrt{19}$ |
18.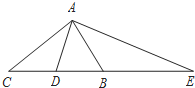 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )| A. | △AED∽△ACB | B. | △AEB∽△ACD | C. | △BAE∽△ACE | D. | △AEC∽△DAC |