题目内容
18.已知定义在[1,+∞)上的函数f(x)=$\left\{\begin{array}{l}4-8|{x-\frac{3}{2}}|,1≤x≤2\\ \frac{1}{2}f(\frac{x}{2}),x>2\end{array}$,给出下列结论:(1)函数f(x)的值域为[0,4];
(2)关于x的方程$f(x)={(\frac{1}{2})^n}$(n∈N*)有2n+4个不相等的实数根;
(3)当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的图形面积为2;
(4)存在x0∈[1,8],使得不等式x0f(x0)>6成立,
其中正确的结论个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由已知解析式,画出函数的图象,进而根据图象分析四个结论的真假,综合分析结果得出答案.
解答 解:当1≤x≤$\frac{3}{2}$时,f(x)=4+8(x-$\frac{3}{2}$)=8x-8;
当$\frac{3}{2}$<x≤2时,f(x)=4-8(x-$\frac{3}{2}$)=-8x+16.
当2<x≤3时,1<$\frac{x}{2}$≤$\frac{3}{2}$,f(x)=$\frac{1}{2}$f($\frac{x}{2}$)=$\frac{1}{2}$(8×$\frac{x}{2}$-8)=2x-4;
当3<x≤4时,$\frac{3}{2}$<$\frac{x}{2}$≤2,f(x)=$\frac{1}{2}$(-8×$\frac{x}{2}$+16)=-2x+8.
当4<x≤6时,2<$\frac{x}{2}$≤3,f(x)=$\frac{1}{2}$(2×$\frac{x}{2}$-4)=$\frac{1}{2}$x-2;
当6<x≤8时,3<$\frac{x}{2}$≤4,f(x)=$\frac{1}{2}$(-2×$\frac{x}{2}$+8)=-$\frac{1}{2}$x+4.….
画出函数f(x)的图象: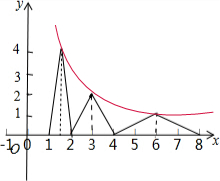
由图象可知:
(1)函数f(x)的值域为[0,4],正确;
(2)当n=1时,关于x的方程f(x)=$\frac{1}{2}$有7个不相等的实根,因此②不正确;
(3)当x∈[2n-1,2n]时,函数f(x)的图象与x轴围成的图形的面积为S,则S=$\frac{1}{2}$×2n-1×23-n=2,正确;
(4)画出函数y=$\frac{6}{x}$(x>0)的图象,可知与函数y=f(x)有交点,
如x=$\frac{3}{2}$,3,6等,因此不存在x0∈[1,8],使得不等式f(x0)>$\frac{6}{{x}_{0}}$即x0f(x0)>6成立,因此不正确.
综上可知:(1)(3)正确.
故正确结论的个数为2个,
故选:B.
点评 本题考查了分段函数的解析式、图象及其性质,考查了分类讨论、数形结合的思想方法,属于难题

| A. | $\sqrt{3}$f($\frac{π}{12}$)<f($\frac{π}{6}$) | B. | f($\frac{1}{4}$)$>2f(\frac{π}{12})$sin$\frac{1}{2}$ | C. | $\sqrt{3}$f($\frac{π}{8}$)>$\sqrt{2}$f($\frac{π}{6}$) | D. | $\sqrt{2}$f($\frac{π}{12}$)>f($\frac{π}{8}$) |
| A. | (-∞,-1)及(0,1) | B. | (-1,0)及(1,+∞) | C. | (-1,1) | D. | (-∞,-1)及(1,+∞) |
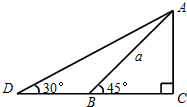 如图,有一条长为a米的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为$\sqrt{2}$a米.
如图,有一条长为a米的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为$\sqrt{2}$a米.