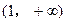题目内容
已知奇函数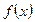 的定义域为实数集
的定义域为实数集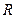 ,且
,且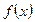 在
在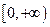 上是增函数,当
上是增函数,当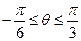 时,是否存在实数
时,是否存在实数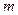 ,使
,使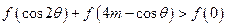 对所有的
对所有的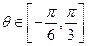 恒成立?若存在,求出实数
恒成立?若存在,求出实数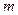 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 的定义域为实数集
的定义域为实数集 ,且
,且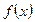 在
在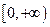 上是增函数,当
上是增函数,当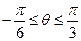 时,是否存在实数
时,是否存在实数 ,使
,使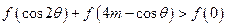 对所有的
对所有的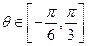 恒成立?若存在,求出实数
恒成立?若存在,求出实数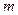 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.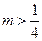
 是奇函数,
是奇函数,
 在
在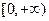 上为增函数,
上为增函数,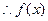 在R上是单调递增函数,
在R上是单调递增函数,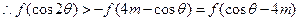 ,
,于是
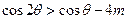 对
对 恒成立,
恒成立,即
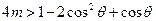 对
对 恒成立.
恒成立.令
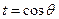 ,
,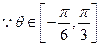 ,
,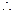
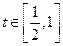 ,则
,则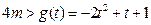 对
对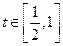 恒成立,故只需
恒成立,故只需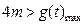 ,而当
,而当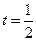 时,
时,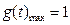 ,于是
,于是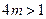 ,解得
,解得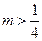 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
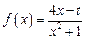 ,已知关于
,已知关于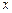 的方程
的方程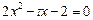 的两个根为
的两个根为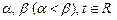 ,
,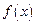 在
在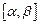 上的单调性;
上的单调性;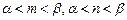 ,证明
,证明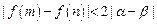 .
.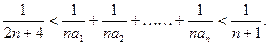
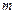 元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?
元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?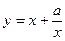 有如下性质:如果常数
有如下性质:如果常数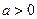 ,那么该函数在(0,
,那么该函数在(0,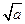 )上减函数,在
)上减函数,在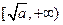 是增函数。
是增函数。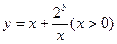 的值域为
的值域为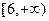 ,求
,求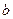 的值;
的值;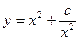 (常数
(常数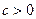 )在定义域的单调性,并说明理由;
)在定义域的单调性,并说明理由;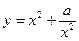 (常数
(常数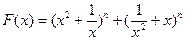 (n是正整数)在区间[
(n是正整数)在区间[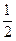 ,2]上的最大值和最小值(可利用你的研究结论)。
,2]上的最大值和最小值(可利用你的研究结论)。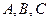 是直线
是直线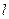 上的三点,点
上的三点,点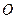 在直线
在直线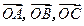 满足
满足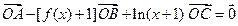 .
.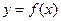 的表达式;
的表达式;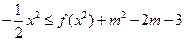 对
对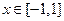 恒成立,求实数
恒成立,求实数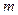 的取值范围
的取值范围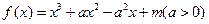 .
.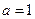 时函数
时函数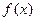 有三个互不相同的零点,求
有三个互不相同的零点,求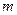 的取值范围;
的取值范围;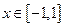 内没有极值点,求
内没有极值点,求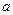 的取值范围;
的取值范围;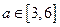 ,不等式
,不等式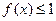 在
在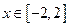 上恒成立,求实数
上恒成立,求实数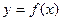 定义域为
定义域为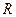 ,当
,当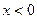 时,
时,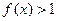 ,且对于任意的
,且对于任意的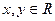 ,都有
,都有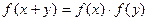
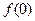 的值,并证明函数
的值,并证明函数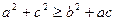 时,不等式
时,不等式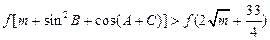 恒成立,求实数
恒成立,求实数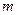 的取值范围。
的取值范围。 的图象恰有两个公共点,则实数a的取值范围是( )
的图象恰有两个公共点,则实数a的取值范围是( )