题目内容
已知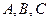 是直线
是直线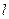 上的三点,点
上的三点,点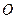 在直线
在直线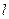 外,向量
外,向量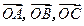 满足
满足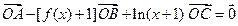 .
.
(Ⅰ)求函数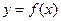 的表达式;
的表达式;
(Ⅱ)若不等式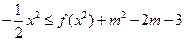 对
对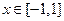 恒成立,求实数
恒成立,求实数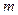 的取值范围
的取值范围
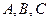 是直线
是直线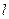 上的三点,点
上的三点,点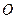 在直线
在直线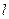 外,向量
外,向量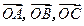 满足
满足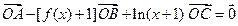 .
.(Ⅰ)求函数
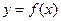 的表达式;
的表达式;(Ⅱ)若不等式
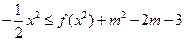 对
对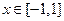 恒成立,求实数
恒成立,求实数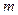 的取值范围
的取值范围(1)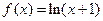 (2)
(2)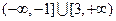
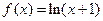 (2)
(2)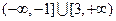
(Ⅰ)∵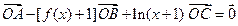 ,
,
∴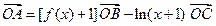 .
.
由于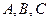 三点共线,∴
三点共线,∴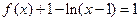 ,∴
,∴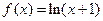 .
.
(Ⅱ)由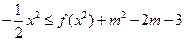 ,
,
得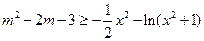 .……①
.……①
令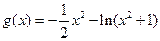 ,
,
∵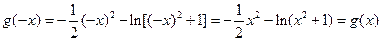 ,
,
∴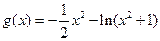 为偶函数.
为偶函数.
又易知,当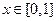 时,
时,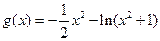 为减函数,
为减函数,
∵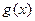 为偶函数,∴
为偶函数,∴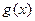 在区间
在区间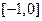 为增函数.
为增函数.
∴当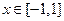 时,
时,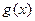 最大值为
最大值为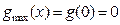 .
.
要使①成立,只需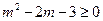 ,解得
,解得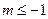 或
或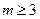 .
.
故所求,实数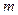 的取值范围是
的取值范围是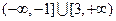
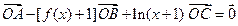 ,
,∴
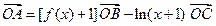 .
.由于
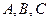 三点共线,∴
三点共线,∴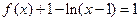 ,∴
,∴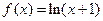 .
.(Ⅱ)由
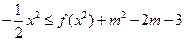 ,
,得
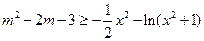 .……①
.……①令
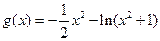 ,
,∵
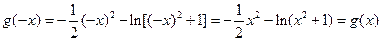 ,
,∴
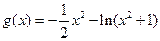 为偶函数.
为偶函数.又易知,当
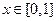 时,
时,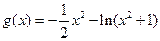 为减函数,
为减函数,∵
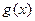 为偶函数,∴
为偶函数,∴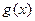 在区间
在区间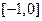 为增函数.
为增函数.∴当
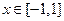 时,
时,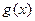 最大值为
最大值为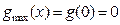 .
.要使①成立,只需
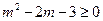 ,解得
,解得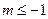 或
或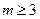 .
.故所求,实数
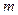 的取值范围是
的取值范围是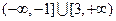

练习册系列答案
相关题目
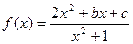
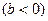 的值域为
的值域为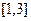 ;
;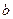 、
、 的值;
的值;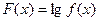 在
在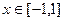 上的单调性,并给出证明;
上的单调性,并给出证明;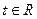 ,求证:
,求证: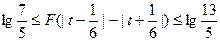 。
。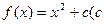 为实常数),且
为实常数),且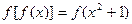 ,其图象和y轴交于A点;数列
,其图象和y轴交于A点;数列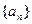 为公差为
为公差为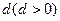 的等差数列,且
的等差数列,且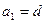 ;点列
;点列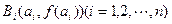
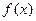 的表达式;
的表达式;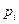 为直线
为直线 的斜率,
的斜率,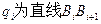 的斜率,求证数
的斜率,求证数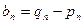 仍为等差数列;
仍为等差数列;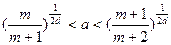 ,求证数列
,求证数列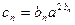 有唯一的最大项.
有唯一的最大项.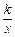 +
+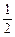 x2在 (0,
x2在 (0,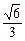 ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;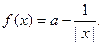
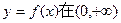 上是增函数.
上是增函数. 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.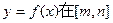 上的值域是
上的值域是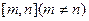 ,求实数a的取值范围.
,求实数a的取值范围.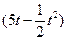 万元
万元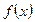 的定义域为实数集
的定义域为实数集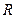 ,且
,且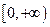 上是增函数,当
上是增函数,当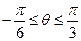 时,是否存在实数
时,是否存在实数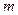 ,使
,使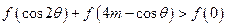 对所有的
对所有的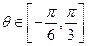 恒成立?若存在,求出实数
恒成立?若存在,求出实数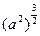 =a3 ②
=a3 ②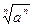 =|a| ③函数y=
=|a| ③函数y=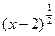 -(3x-7)0的定义域是(2, +∞) ④若
-(3x-7)0的定义域是(2, +∞) ④若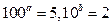 ,则2a+b=1
,则2a+b=1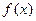 是
是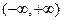 上的偶函数,若对于
上的偶函数,若对于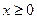 ,都有
,都有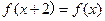 ,且当
,且当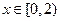 时,
时,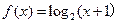 ,则
,则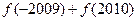 的值为 ( )
的值为 ( )