题目内容
设函数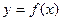 定义域为
定义域为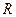 ,当
,当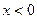 时,
时,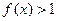 ,且对于任意的
,且对于任意的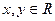 ,都有
,都有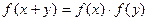
(1)求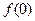 的值,并证明函数
的值,并证明函数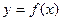 在
在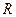 上是减函数;
上是减函数;
(2)记△ABC的三内角A、B、C的对应边分别为a,b,c,若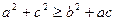 时,不等式
时,不等式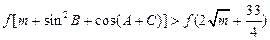 恒成立,求实数
恒成立,求实数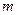 的取值范围。
的取值范围。
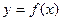 定义域为
定义域为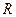 ,当
,当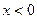 时,
时,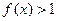 ,且对于任意的
,且对于任意的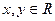 ,都有
,都有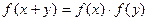
(1)求
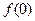 的值,并证明函数
的值,并证明函数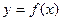 在
在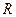 上是减函数;
上是减函数;(2)记△ABC的三内角A、B、C的对应边分别为a,b,c,若
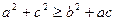 时,不等式
时,不等式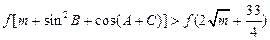 恒成立,求实数
恒成立,求实数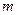 的取值范围。
的取值范围。 (1)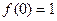 ,
,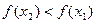 ,故函数
,故函数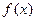 在
在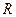 上是减函数。
上是减函数。
(2)
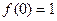 ,
,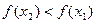 ,故函数
,故函数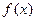 在
在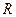 上是减函数。
上是减函数。(2)

(1)
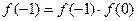 ,且当
,且当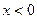 时,
时,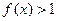 ,所以
,所以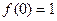
当
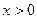 时,
时,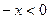 ,
,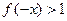 ,
,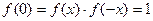 ,
, 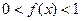
对于
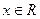 ,
,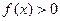 ,设
,设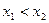 ,
,则
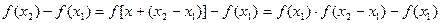
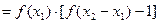
又
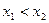 ,所以
,所以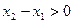 ,
,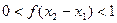 ,
,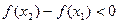 ,
,即
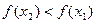 ,故函数
,故函数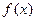 在
在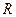 上是减函数。
上是减函数。(2)
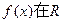 上单调递减,且
上单调递减,且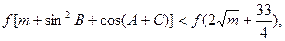
所以
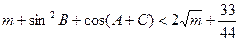
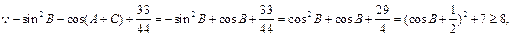


练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 (a<0,
(a<0,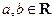 ,设关于x的方程
,设关于x的方程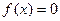 的两根为
的两根为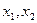 ,
,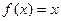 的两实根为
的两实根为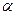 、
、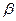 . (1)若
. (1)若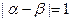 ,求a,b关系式
,求a,b关系式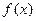 解析式
解析式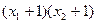 <7
<7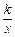 +
+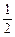 x2在 (0,
x2在 (0,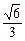 ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;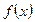 的定义域为实数集
的定义域为实数集 ,且
,且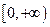 上是增函数,当
上是增函数,当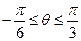 时,是否存在实数
时,是否存在实数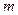 ,使
,使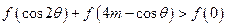 对所有的
对所有的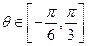 恒成立?若存在,求出实数
恒成立?若存在,求出实数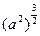 =a3 ②
=a3 ②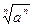 =|a| ③函数y=
=|a| ③函数y=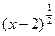 -(3x-7)0的定义域是(2, +∞) ④若
-(3x-7)0的定义域是(2, +∞) ④若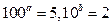 ,则2a+b=1
,则2a+b=1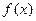 的解析式;(2)用定义证明
的解析式;(2)用定义证明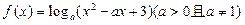 ,满足对任意的
,满足对任意的 、
、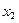 ,当
,当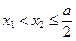 时,
时,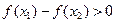 ,则实数
,则实数 的取值范围为( )
的取值范围为( )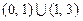
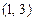
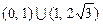
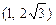
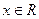 ,
,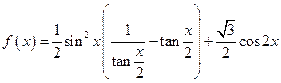 .
.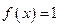 ,求
,求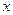 的值.
的值.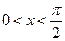 ,求
,求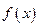 的单调的递减区间;
的单调的递减区间;